hdu3499---玄学的分层图

枚举固然可以，但是我还是想看看分层图。。。。

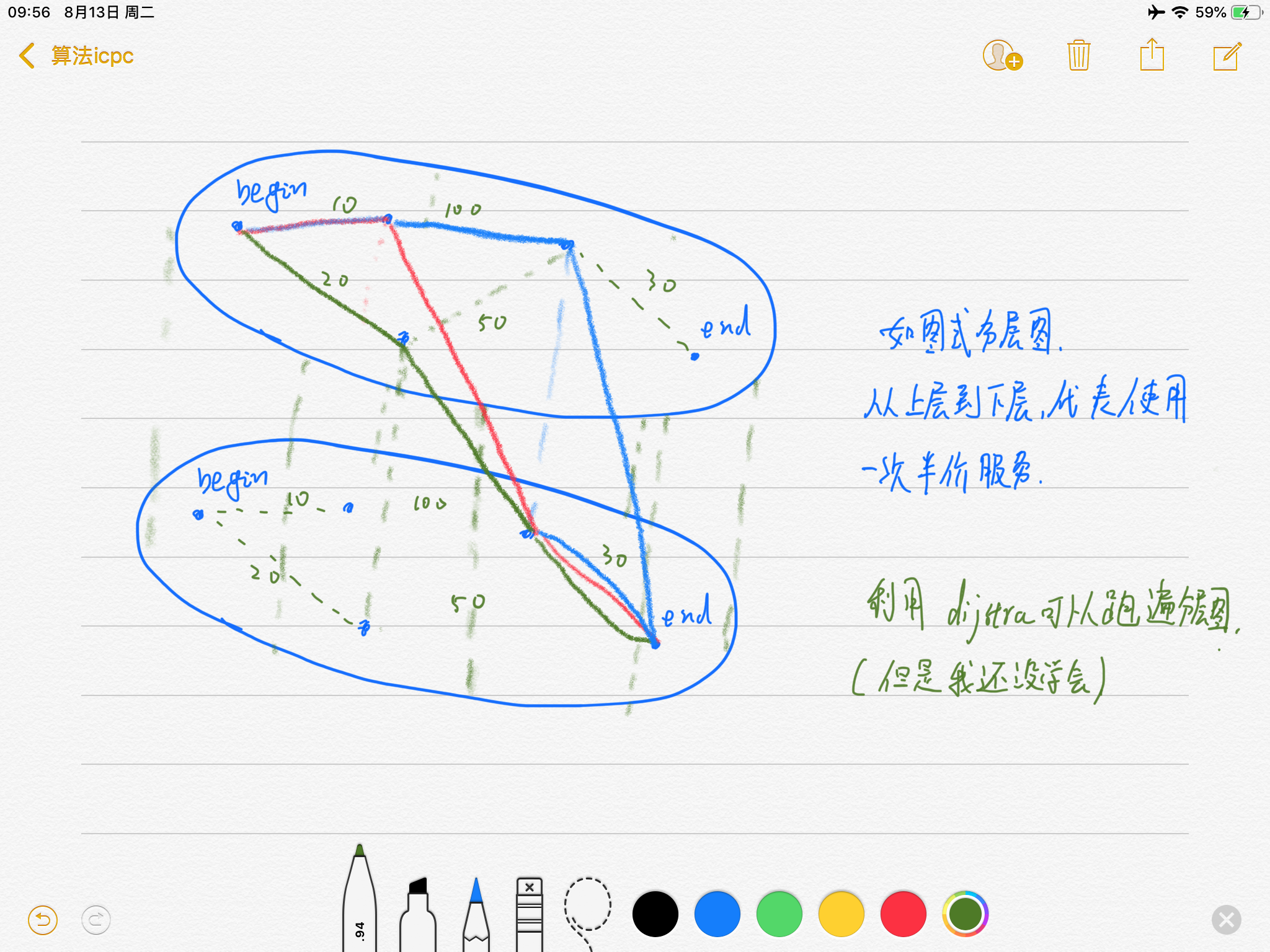
如本题所述 ，从上图到下图就是一个折扣的过程，上部分只有一种办法下去，下部分图没有办法去上面，该模型十分的巧妙啊！！！

下面我来演示一下自己改的样例吧

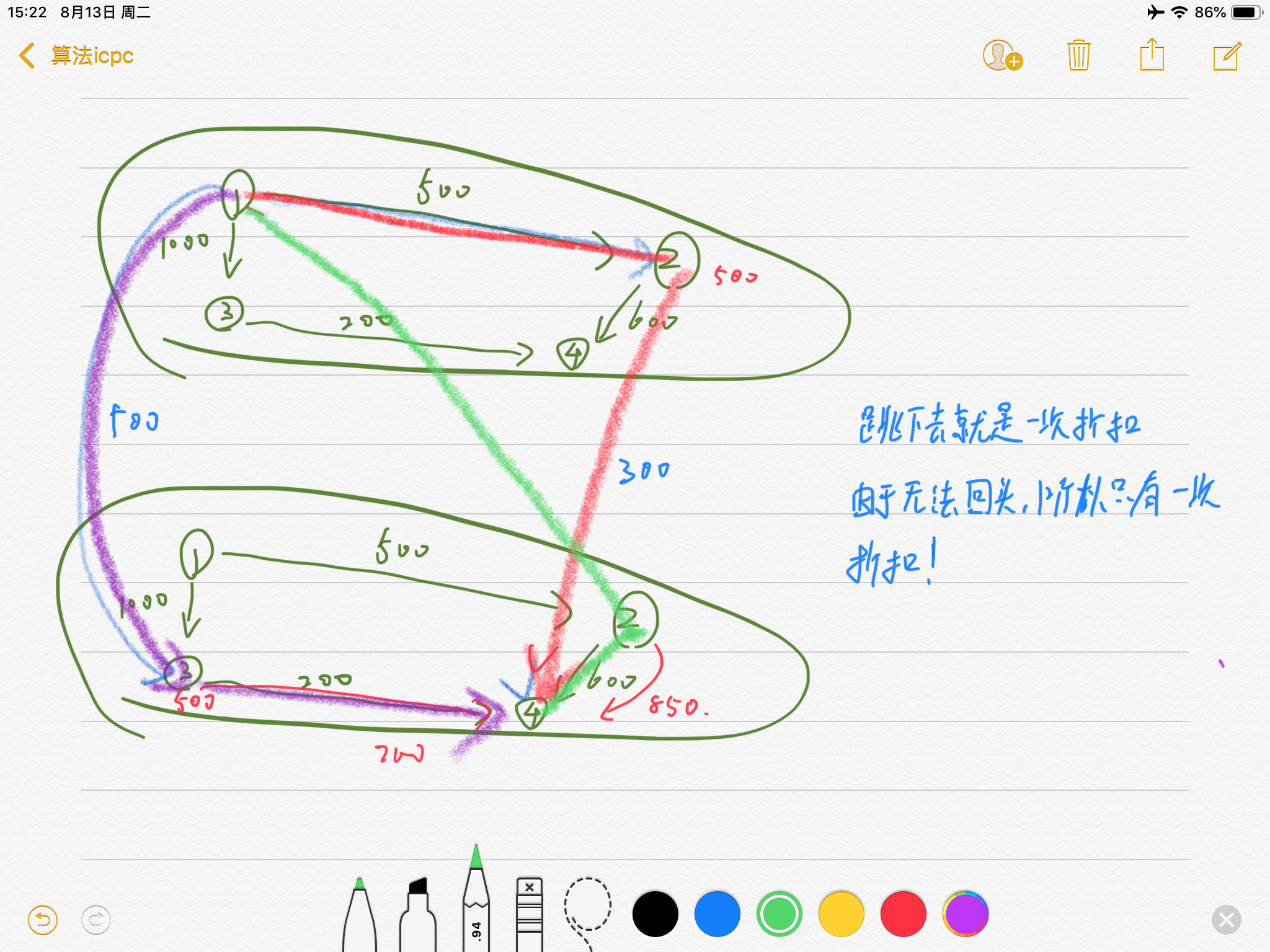
紫色路线是最短的，从上往下的路就是打折的路，类似bfs搜索，上面的所有点都可以下来，但是dijkstra只会只会保留最优的解

#include<cstring>
#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
#include<map>
#include<string>
using namespace std;
#define maxn 500000+10
typedef long long ll;
const long long INF = 2e14;
struct Node {
	int p, tmp;
	ll val;
	Node(int a, ll b,int t) :p(a), val(b),tmp(t) {}
};
int n, m;
vector<Node>G[maxn];
bool operator < (const Node a, const Node b) {
	if (a.val > b.val) return true;
	else return false;
}
int vis[maxn][2];
ll dis[maxn][2];
void insert(int be, int en, ll len) {
	G[be].push_back(Node(en, len, 0));
	G[be].push_back(Node(en, len, 1));
	return;
}
int dijkstra(int be) {
	priority_queue<Node>que;
	for (int i = 0; i <= n; i++) {
		for (int j = 0; j < 2; j++) {
			vis[i][j] = 0;
			dis[i][j] = INF;
		}
	}
	dis[be][0] = 0;
	dis[be][1] = 0;
	que.push(Node(be, 0, 0));
	while (!que.empty()) {
		Node ans = que.top();
		que.pop();
		if (vis[ans.p][ans.tmp] == 0) {
			vis[ans.p][ans.tmp] = 1;
			for (int i = 0; i < G[ans.p].size(); i++) {
				int p = G[ans.p][i].p;
				int t = G[ans.p][i].tmp;//确定位置
				if (!vis[p][t] && dis[p][t] > dis[ans.p][t] + G[ans.p][i].val) {
					dis[p][t] = G[ans.p][i].val + dis[ans.p][t];
					que.push(Node(p, dis[p][t], t));
				}

				if (t == 0) {//可以下来的话
					if (!vis[p][1] && dis[p][1] > dis[ans.p][0] + G[ans.p][i].val / 2) {//从上面穿下来所以是0加给1
						dis[p][1] = dis[ans.p][0] + G[ans.p][i].val/2;
						que.push(Node(p, dis[p][1], 1));
					}
				}
			}
		}
	}
	return 0;
}
map<string, int>ins;
int main() {
	while (~scanf("%d %d", &n, &m)) {
		ins.clear();
		for (int i = 0; i <= n; i++)G[i].clear();
 		string be, en;
		ll len;
		int cnt = 1;
		while (m--) {
			cin >> be >> en;
			scanf("%lld", &len);
			if (ins[be] == 0) ins[be] = cnt++;
			if (ins[en] == 0) ins[en] = cnt++;
			insert(ins[be], ins[en], len);
		}
		cin >> be >> en;
		if (ins[be] == 0) ins[be] = cnt++;
		if (ins[en] == 0) ins[en] = cnt++;
		dijkstra(ins[be]);
		if (dis[ins[en]][1] == INF) printf("-1\n");
		else printf("%lld\n", dis[ins[en]][1]);
	}
	return 0;
}