ZH奶酪：【数据结构与算法】基础排序算法总结与Python实现

1、冒泡排序（BubbleSort）

介绍：重复的遍历数列，一次比较两个元素，如果他们顺序错误就进行交换。

2016年1月22日总结：

冒泡排序就是比较相邻的两个元素，保证每次遍历最后的元素最大。

排序过程需要用到：int i,j;

 def bubble_sort(arry):
     n = len(arry)                   #获得数组的长度
     for i in range(n):
         for j in range(1,n-i):
             if  arry[j-1] > arry[j] :       #如果前者比后者大
                 arry[j-1],arry[j] = arry[j],arry[j-1]      #则交换两者
     return arry

优化方案：

（1）某一趟遍历如果没有数据交换，则说明已经排好了；

（2）记录某次遍历时最后发生数据交换的位置，这个位置之后的数据显然已经有序了，不用再排序了；

2、选择排序（SelectionSort）

介绍：从未排序的数列中找到最小（大）的元素，放在数列的起始（末尾），直到整个数列都进行了排序；

2016年1月22日总结：

选择排序就是每次迭代选择最大值，然后放到最后。

排序过程需要用到：int i,j; 和 int temp（保存最大值）;

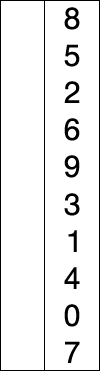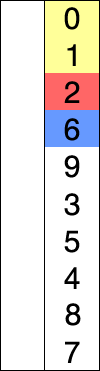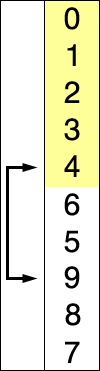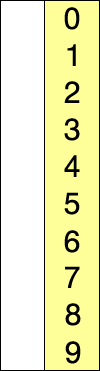
 def select_sort(ary):
     n = len(ary)
     for i in range(0,n):
         min = i                             #最小元素下标标记
         for j in range(i+1,n):
             if ary[j] < ary[min] :
                 min = j                     #找到最小值的下标
         ary[min],ary[i] = ary[i],ary[min]   #交换两者
     return ary

3、插入排序（InsertionSort）

介绍：一个有序数列，一个无序数列，遍历无序数列，把数据插入到有序数列的相应位置；

2016年1月22日总结：

插入排序就是把无序数列依次插入有序数列

排序过程需要用到int i,j;和int idx（用来保存下标）;

 def insert_sort(ary):
     n = len(ary)
     for i in range(1,n):
         if ary[i] < ary[i-1]:
             temp = ary[i]
             index = i           #待插入的下标
             for j in range(i-1,-1,-1):  #从i-1 循环到 0 (包括0)
                 if ary[j] > temp :
                     ary[j+1] = ary[j]
                     index = j   #记录待插入下标
                 else :
                     break
             ary[index] = temp
     return ary

4、希尔排序（ShellSort）

介绍：也称为递减增量排序算法，实质是分组插入排序。希尔排序是非稳定排序算法。

2016年1月22日总结：

希尔排序就是分组插入排序，主要有两点：一个是控制分组，一个是插入排序。

基本思想：将数组列在一个表中，对表的每列进行插入排序，重复这个过程，每次增加列的长度，直到最后只有一列。（把数组说成是表是为了更好理解这个算法，算法本身还是用数组进行排序）

例如，有数组 [ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ] ，我们先以步长为5进行排序，我们可以通过将数组放到有5列的表中进行观察：

13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10

然后对每列进行插入排序：

10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45

这时候数组实际上是这样的： [ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ] 。这时10已经处于正确位置了，然后再以步长3进行排序：

10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45

对每列进行插入排序之后是这样的：

10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94

最后以步长1排序（就是简单的插入排序了）

 def shell_sort(ary):
     n = len(ary)
     gap = round(n/2)       #初始步长 , 用round四舍五入取整
     while gap > 0 :
         for i in range(gap,n):        #每一列进行插入排序 , 从gap 到 n-1
             temp = ary[i]
             j = i
             while ( j >= gap and ary[j-gap] > temp ):    #插入排序
                 ary[j] = ary[j-gap]
                 j = j - gap
             ary[j] = temp
         gap = round(gap/2)                     #重新设置步长
     return ary

上面源码的步长的选择是从n/2开始，每次再减半，直至为0。步长的选择直接决定了希尔排序的复杂度。（维基百科上的代码）

 void shell_sort(int arr[], int len) {
     int gap, i, j;
     int temp;
     for (gap = len >> ; gap > ; gap >>= )
         for (i = gap; i < len; i++) {
             temp = arr[i];
             for (j = i - gap; j >=  && arr[j] > temp; j -= gap)
                 arr[j + gap] = arr[j];
             arr[j + gap] = temp;
         }
 }

希尔排序动画演示

http://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html

5、归并排序（MergeSort）

介绍：归并排序是采用分治法的一个典型应用。

2016年1月22日总结：

归并排序，主要有两步：分解+合并

基本思想：先递归分解数组，再合并数组；

　　先考虑简单一点的，合并两个有序数组，基本思路就是比较两个数组的最前面的数，谁小就取谁，取了后相应的指针就往后移一位，然后再比较，直至一个数组为空，最后把一个数组剩余部分复制过来即可。

　　再考虑把上述问题进行递归分解，基本思路就是将数组分解成left和right两部分，如果这两个数组内部的数据是有序的，那么就可以用上面合并数组的方法将这个两个数组合并排序。如何让这两个数组内部是有序的呢？可以再二分，直至分解出的小组只含有一个元素位置，此时认为该小组内部有序，然后合并排序相邻的两个小组即可。

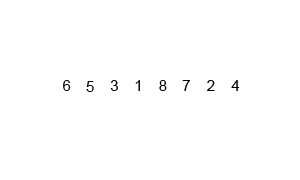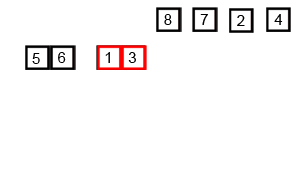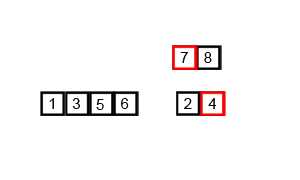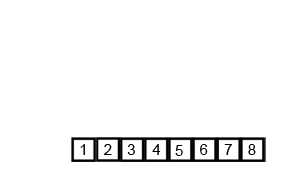
C++递归版本（维基百科）

 template<typename T>
 void merge_sort_recursive(T arr[], T reg[], int start, int end) {
     if (start >= end)
         return;
     int len = end - start, mid = (len >> ) + start;
     int start1 = start, end1 = mid;
     int start2 = mid + , end2 = end;
     merge_sort_recursive(arr, reg, start1, end1);
     merge_sort_recursive(arr, reg, start2, end2);
     int k = start;
     while (start1 <= end1 && start2 <= end2)
         reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
     while (start1 <= end1)
         reg[k++] = arr[start1++];
     while (start2 <= end2)
         reg[k++] = arr[start2++];
     for (k = start; k <= end; k++)
         arr[k] = reg[k];
 }
 template<typename T> //整數或浮點數皆可使用,若要使用物件(class)時必須設定"小於"(<)的運算子功能
 void merge_sort(T arr[], const int len) {
     T reg[len];
     merge_sort_recursive(arr, reg, , len - );
 }

Python

 def merge_sort(ary):
     if len(ary) <= 1 : return ary
     num = int(len(ary)/2)       #二分分解
     left = merge_sort(ary[:num])
     right = merge_sort(ary[num:])
     return merge(left,right)    #合并数组

 def merge(left,right):
     '''合并操作，
     将两个有序数组left[]和right[]合并成一个大的有序数组'''
     l,r = 0,0           #left与right数组的下标指针
     result = []
     while l<len(left) and r<len(right) :
         if left[l] < right[r]:
             result.append(left[l])
             l += 1
         else:
             result.append(right[r])
             r += 1
     result += left[l:]
     result += right[r:]
     return result

6、快速排序（QuickSort）

介绍：

快速排序通常明显比同为O(n*log_n)的其他算法更快，因此常被采用，而且快排也采用了分治法的思想，所以在很多笔试面试中经常看到快排的影子。

2016年1月22日总结：

快速排序主要有两步：排序+递归

（1）从数列中挑出一个元素作为基准数；

（2）分区过程，将比基数大的放到右边，小于或等于基数的放到左边；

（3）再对左右区间递归执行（2），直至各区间只有一个数；

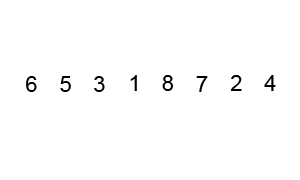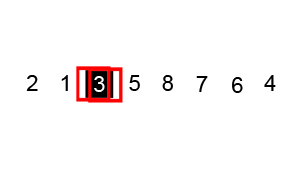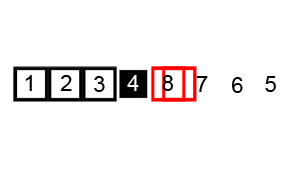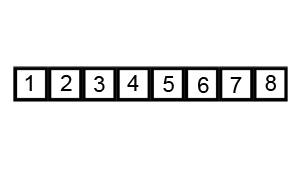
 def quick_sort(ary):
     return qsort(ary,0,len(ary)-1)

 def qsort(ary,left,right):
     #快排函数，ary为待排序数组，left为待排序的左边界，right为右边界
     if left >= right : return ary
     key = ary[left]     #取最左边的为基准数
     lp = left           #左指针
     rp = right          #右指针
     while lp < rp :
         while ary[rp] >= key and lp < rp :
             rp -= 1
         while ary[lp] <= key and lp < rp :
             lp += 1
         ary[lp],ary[rp] = ary[rp],ary[lp]
     ary[left],ary[lp] = ary[lp],ary[left]
     qsort(ary,left,lp-1)
     qsort(ary,rp+1,right)
     return ary

7、堆排序（HeapSort）

介绍：

堆排序在top K问题中使用比较频繁。堆排序是采用二叉堆的数据结构来实现的，虽然实质上还是一维数组。二叉堆是一个近似完全二叉树。

2016年1月22日总结：

堆排序，首先要理解二叉堆（近似完全二叉树），把无序数组看成二叉堆的层次遍历；

然后从最后一个父节点开始调整二叉堆为最大堆，这是根节点是最大的元素；

接着把根节点和二叉堆中最后一个元素互换位置，这是最大的元素就在数组的后边，而最后一个元素变成了根元素，二叉堆的结点数就相当于少了一个；然后调整新的二叉堆（比之前的二叉堆少了一个元素）；重复这步；

二叉堆有以下性质：

（1）父节点的键值总是大于（小于）或等于任何一个子节点的键值；

（2）每个节点的左右子树都是一个二叉堆

步骤：

（1）构造最大堆（Build_Max_Heap）：若数组下标范围为0~n，考虑到单独一个元素是大根堆，则从下标n/2开始的元素均为大根堆。于是只要从n/2-1开始，向前一次构造大根堆，这样就能保证，构造到某个节点时，它的左右子树都已经是大根堆；

（2）堆排序（HeapSort）：由于堆是用数组模拟的，得到一个大根堆后，数组内部并不是有序的。因此需要将堆化数组有序化。

　　思想是：移除根节点并做最大堆调整的递归运算。

　　第一次将heap[0]和heap[n-1]交换，再对heap[0...n-2]做最大堆调整。

　　第二次将heap[0]和heap[n-2]交换，再对heap[0...n-3]  做最大堆调整。

　　重复上述操作直至heap[0]与heap[1]交换。

　　由于每次都是将最大的数并入到后面的有序区间，故操作完后整个数组就是有序的了。

（3）最大堆调整（Max_Heapify）：该方法是提供给上述两个过程调用的。目的是将堆的末端子节点做调整，似的子节点永远小于父节点。

另一个动画演示（可以自定义参数）：http://www.cs.usfca.edu/~galles/visualization/flash.html

 def heap_sort(ary) :
     n = len(ary)
     first = int(n/2-1)       #最后一个非叶子节点
     for start in range(first,-1,-1) :     #构造大根堆
         max_heapify(ary,start,n-1)
     for end in range(n-1,0,-1):           #堆排，将大根堆转换成有序数组
         ary[end],ary[0] = ary[0],ary[end]
         max_heapify(ary,0,end-1)
     return ary

 #最大堆调整：将堆的末端子节点作调整，使得子节点永远小于父节点
 #start为当前需要调整最大堆的位置，end为调整边界
 def max_heapify(ary,start,end):
     root = start
     while True :
         child = root*2 +1               #调整节点的子节点
         if child > end : break
         if child+1 <= end and ary[child] < ary[child+1] :
             child = child+1             #取较大的子节点
         if ary[root] < ary[child] :     #较大的子节点成为父节点
             ary[root],ary[child] = ary[child],ary[root]     #交换
             root = child
         else :
             break

总结

上述七种排序算法的对比：

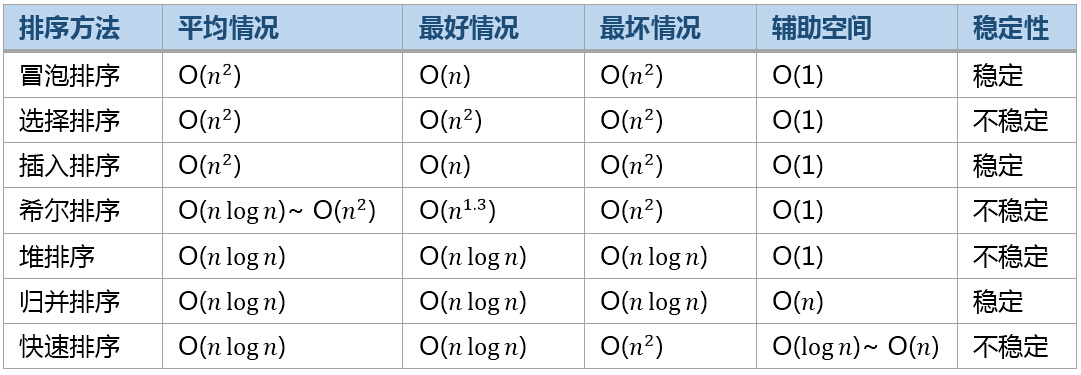
原文链接：http://wuchong.me/blog/2014/02/09/algorithm-sort-summary/