Summary: Lowest Common Ancestor in a Binary Tree & Shortest Path In a Binary Tree

转自：Pavel's Blog

Now let's say we want to find the LCA for nodes 4 and 9, we will need to traverse the whole tree to compare each node so that we can locate the nodes. Now considering that we start the traversal with the left branch (pre-order traversal) - we have the worst case here with O(n) running time.

Traversing the tree we compare the current node with both of the nodes and if one of them match, it means that one is the LCA on the respective branch. Let's say after traversing the above tree in pre-order  the first node that matches our nodes is 9 (2, 7, 2, 6, 5, 11, 5, 9). So the first obvious thought is that the 4 must be a child of 9, since we're already on the right child of node 5 and the pre-order traversal looks at the node first, then the left child and lastly the right child. Then we note node 9 as the LCA and we don't have to look further anymore.

 

Let's use another case, say we're looking for the LCA of 7 and 9. The first node in our pre-order traversal (2, 7, 2, 6, 5, 11, 5, 9, 4) is 7. Now here we can say that the LCA for the left branch is 7 because again, if the second node is in the same branch, independently of where and how deep it will be in this branch, the LCA will still be 7; thus we don't have to look in this branch anymore. But we still did not look at the right branch, so we keep traversing in a pre-order manner, but now omitting the other nodes: 2, 7, 5, 9. Now we can say that the LCA for that branch is 9. We can also affirm that the LCA for the branch with the root in node 5 is also 9. And in the end we have our nodes both in separate branches, which means that the LCA is the root of those branches - node 2.

 

The algorithm looks as a modified version of a pre-order tree traversal :

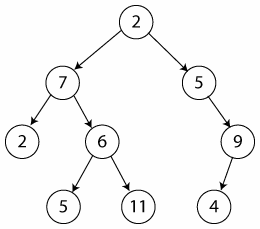 public static Node lowestCommonAncestor(Node root, Node a, Node b) {
     if (root == null) {
         return null;
     }
 
     if (root.equals(a) || root.equals(b)) {
         // if at least one matched, no need to continue
         // this is the LCA for this root
         return root;
     }
 
     Node l = lowestCommonAncestor(root.left, a, b);
     Node r = lowestCommonAncestor(root.right, a, b);
 
     if (l != null && r != null) {
         return root;  // nodes are each on a seaparate branch
     }
 
     // either one node is on one branch,
     // or none was found in any of the branches
     return l != null ? l : r;
 }

For the node used we will use the following class:

 public class Node {
     public int data;
     public Node right;
     public Node left;
 
     public Node(int data) {
         this.data = data;
     }
 }

这个问题再follow up一下，就是要找到shortest path in a binary tree between two nodes

 public class Solution {
     public static List<Node> shortestPath(Node root, Node a, Node b) {
         ArrayList<Node> path1 = new ArrayList<Node>();
         ArrayList<Node> path2 = new ArrayList<Node>();
         Node LCA = lowestCommonAncestor(root, a, b);
         helper(LCA.left, a, b, path1, new ArrayList<Node>());
         helper(LCA.right, a, b, path2, new ArrayList<Node>());
         Collections.reverse(path1);
         path1.add(LCA);
         path1.addAll(new ArrayList<Node>(path2));
         return path1;
     }
 
     public void helper(Node root, Node a, Node b, ArrayList<Node> outpath, ArrayList<Node> temp) {
         if (root == null) return;
         temp.add(root);
         if (root == a || root == b) {
             outpath = new ArrayList<Node>(temp);
             return;
         }
         helper(root.left, a, b, outpath, temp);
         helper(root.right, a, b, outpath, temp);
         temp.remove(temp.size()-1);
     }
 }

别人的Stack做法，未深究 他说First stack is not really needed, a simple list would do - I just like symmetry.

 public static <V> void shortestpath(
         Node<V> root, Node<V> a, Node<V> b,
         Stack<Node<V>> outputPath) {
     if (root == null) {
         return;
     }
     if (root.data.equals(a.data) || root.data.equals(b.data)) {
         outputPath.push(root);
         return;
     }
 
     shortestpath(root.left, a, b, outputPath);
     shortestpath(root.right, a, b, outputPath);
 
     outputPath.push(root);
 }
 
 public static List<Node> shortestPath(Node root, Node a, Node b) {
     Stack<Node> path1 = new Stack<>();
     Stack<Node> path2 = new Stack<>();
 
     Node lca = lowestCommonAncestor(root, a, b);
 
     // This is to handle the case where one of the nodes IS the LCA
     Node r = lca.equals(a) ? a : (lca.equals(b) ? b : lca);
 
     shortestpath(r.left, a, b, path1);
     shortestpath(r.right, a, b, path2);
 
     path1.push(r);
     // invert the second path
     while (!path2.isEmpty()) {
         path1.push(path2.pop());
     }
     return path1;
 }