【BZOJ3774】最优选择 最小割

【BZOJ3774】最优选择

Description

小N手上有一个N*M的方格图，控制某一个点要付出Aij的代价，然后某个点如果被控制了，或者他周围的所有点(上下左右)都被控制了，那么他就算是被选择了的。一个点如果被选择了，那么可以得到Bij的回报，现在请你帮小N选一个最优的方案，使得回报-代价尽可能大。

Input

第一行两个正整数N,M表示方格图的长与宽。

接下来N行每行M个整数Aij表示控制的代价。

接下来N行每行M个整数Bij表示选择的回报。

Output

一个整数，表示最大的回报-代价(如果一个都不控制那么就是0)。

Sample Input

3 3
1 100 100
100 1 100
1 100 100
2 0 0
5 2 0
2 0 0

Sample Output

8

HINT

对于100%的数据，N,M<=50，Aij,Bij都是小于等于100的正整数。

题解：忠告：不要看大爷的图！大爷说的挺明白，然后自己想了一个差不多的建图方法，一看大爷的图：这啥玩应？我和大爷建的不一样啊！一定是我错了！然后试图理解大爷的建图方法，得出结论：大爷太神了，这方法我理解不了。

还是来一个不那么神的，又好想又好理解的做法吧！

黑白染色是显然的啦，对于白点，我们钦定划分到T集代表选，然后讨论所有的情况：

1.四周选，当前点不选。划分到S集，代价0。

因为四周的点是黑点，划分到S集代表不选，而将当前点直接连向四周的点即可保证当前点与T集割开，所以连从当前点到四周的点，容量inf的边。

2.四周不选，当前点选。划分到T集，代价A。

我们需要让当前点花费A的代价即可以与S集割开，所以连从S到当前点，容量为A的边即可。

3.四周不选，当前点不选。划分到S集，代价B。

我们需要让当前点花费B的代价即可以与T割开，这个条件和情况1属于【或】关系，所以我们新建点b，设原来的是点a，将1中的边改为从b到四周的点，然后连从a到b，容量为B的边即可。

最终的图其实长这样：

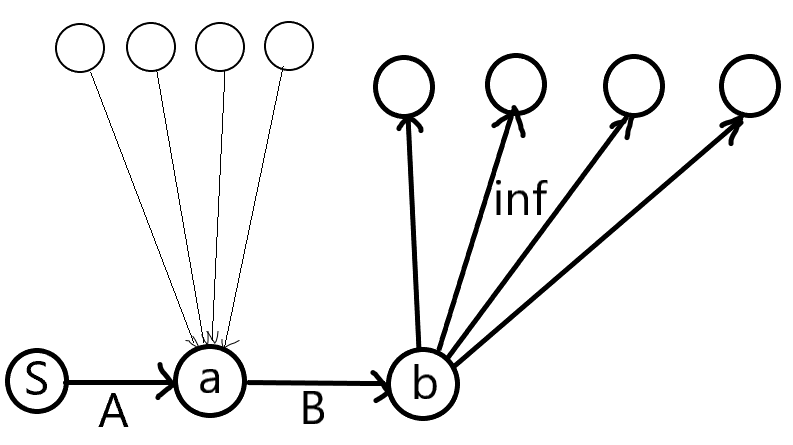
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
#include <algorithm>
#define P(X,Y) ((X-1)*m+Y)
#define inf 1<<30
using namespace std;
int n,m,S,T,ans,cnt;
int A[60][60],B[60][60];
int to[100010],next[100010],head[100010],val[100010],d[10010];
int dx[]={0,1,0,-1},dy[]={1,0,-1,0};
queue<int> q;
inline void add(int a,int b,int c)
{
	to[cnt]=b,val[cnt]=c,next[cnt]=head[a],head[a]=cnt++;
	to[cnt]=a,val[cnt]=0,next[cnt]=head[b],head[b]=cnt++;
}
inline int rd()
{
	int ret=0,f=1;	char gc=getchar();
	while(gc<'0'||gc>'9')	{if(gc=='-')	f=-f;	gc=getchar();}
	while(gc>='0'&&gc<='9')	ret=ret*10+gc-'0',gc=getchar();
	return ret*f;
}
inline int dfs(int x,int mf)
{
	if(x==T)	return mf;
	int i,temp=mf,k;
	for(i=head[x];i!=-1;i=next[i])	if(val[i]&&d[to[i]]==d[x]+1)
	{
		k=dfs(to[i],min(temp,val[i]));
		if(!k)	d[to[i]]=0;
		temp-=k,val[i]-=k,val[i^1]+=k;
		if(!temp)	break;
	}
	return mf-temp;
}
inline int bfs()
{
	memset(d,0,sizeof(d));
	while(!q.empty())	q.pop();
	d[S]=1,q.push(S);
	int i,u;
	while(!q.empty())
	{
		u=q.front(),q.pop();
		for(i=head[u];i!=-1;i=next[i])	if(val[i]&&!d[to[i]])
		{
			d[to[i]]=d[u]+1;
			if(to[i]==T)	return 1;
			q.push(to[i]);
		}
	}
	return 0;
}
int main()
{
	n=rd(),m=rd(),S=0,T=2*n*m+1;
	int i,j,k,a,b,c;
	memset(head,-1,sizeof(head));
	for(i=1;i<=n;i++)	for(j=1;j<=m;j++)	A[i][j]=rd();
	for(i=1;i<=n;i++)	for(j=1;j<=m;j++)	B[i][j]=rd(),ans+=B[i][j];
	for(i=1;i<=n;i++)	for(j=1;j<=m;j++)
	{
		if((i^j)&1)
		{
			a=P(i,j),b=P(i,j)+n*m;
			add(S,a,A[i][j]),add(a,b,B[i][j]);
			for(k=0;k<4;k++)	if(i+dx[k]&&i+dx[k]<=n&&j+dy[k]&&j+dy[k]<=m)
			{
				c=P(i+dx[k],j+dy[k]),add(b,c,inf);
			}
		}
		else
		{
			a=P(i,j),b=P(i,j)+n*m;
			add(a,T,A[i][j]),add(b,a,B[i][j]);
			for(k=0;k<4;k++)	if(i+dx[k]&&i+dx[k]<=n&&j+dy[k]&&j+dy[k]<=m)
			{
				c=P(i+dx[k],j+dy[k]),add(c,b,inf);
			}
		}
	}
	while(bfs())	ans-=dfs(0,inf);
	printf("%d",ans);
	return 0;
}