poj 3111 K Best (二分搜索之最大化平均值之01分数规划)

Description

Demy has n jewels. Each of her jewels has some value vi and weight wi.

Since her husband John got broke after recent financial crises, Demy has decided to sell some jewels. She has decided that she would keep k best jewels for herself. She decided to keep such jewels that their specific value is as large as possible. That is, denote the specific value of some set of jewels S = {i1, i2, …, ik} as

.

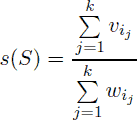Demy would like to select such k jewels that their specific value is maximal possible. Help her to do so.

Input

The first line of the input file contains n — the number of jewels Demy got, and k — the number of jewels she would like to keep ( ≤ k ≤ n ≤  ).

The following n lines contain two integer numbers each — vi and wi ( ≤ vi ≤ ,  ≤ wi ≤ , both the sum of all vi and the sum of all wi do not exceed ).

Output

Output k numbers — the numbers of jewels Demy must keep. If there are several solutions, output any one.

Sample Input

Sample Output

Source

Northeastern Europe 2005, Northern Subregion

 

这题和上一题基本上一样。只是要注意数的大小，数太大的话会超时

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<math.h>
 #include<stdlib.h>
 using namespace std;
 #define N 100006
 #define inf 1<<26
 int n,k;
 double x;
 struct Node{
     double v,w;
     int id;
     bool friend operator < (Node a,Node b){
         return a.v-x*a.w>b.v-x*b.w;
     }
 }node[N];
 bool solve(double mid){
     x=mid;
     sort(node,node+n);
     double sum1=;
     double sum2=;
     for(int i=;i<k;i++){
         sum1+=node[i].v;
         sum2+=node[i].w;
     }
     return sum1/sum2>=mid;
 }
 int main()
 {
     while(scanf("%d%d",&n,&k)==){
         for(int i=;i<n;i++){
             scanf("%lf%lf",&node[i].v,&node[i].w);
             node[i].id=i;
         }

         double low=;
         double high=inf;
         for(int i=;i<;i++){
             double mid=(low+high)/;
             if(solve(mid)){
                 low=mid;
             }
             else{
                 high=mid;
             }
         }
         for(int i=;i<k;i++){
             printf("%d ",node[i].id+);
         }
         printf("\n");
     }
     return ;
 }