界面重建——Marching cubes算法

一、引子

对于一个标量场数据，我们可以描绘轮廓(Contouring)，包括2D和3D。2D的情况称为轮廓线（contour lines），3D的情况称为表面（surface）。他们都是等值线或等值面。

以下是一个2D例子：

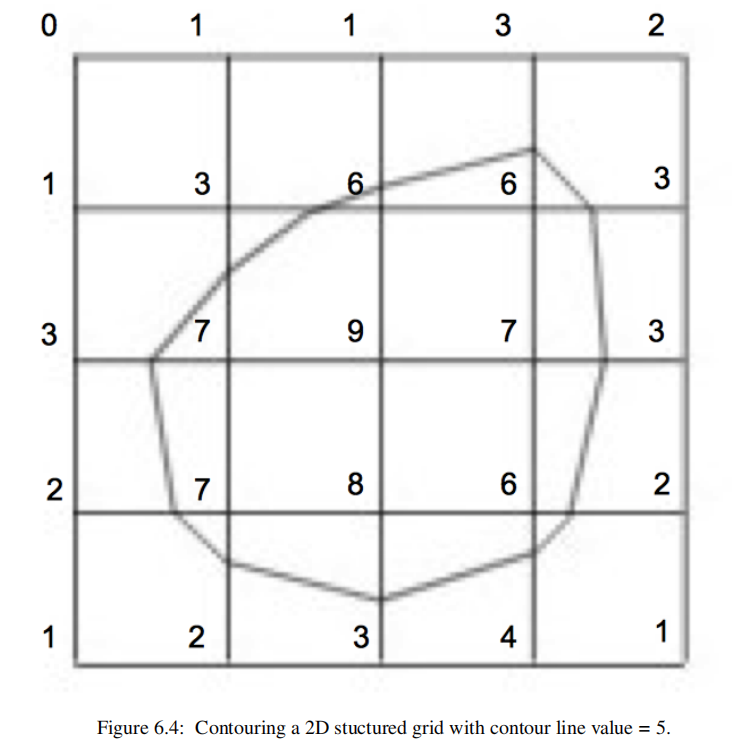
为了生成轮廓，必须使用某种形式的插值。这是因为我们只在数据集中的一个有限点集上有标量值，而我们的等高线值可能位于这两个点的值之间。由于最常见的插值技术是线性插值，我们通过沿边缘的线性插值在轮廓表面上生成点。如果一条边在其两个端点上有标量值10和0，如果我们试图生成一条值为5的等高线，则边缘插值计算该等高线通过边缘的中点。

二、Marching cubes算法——从2D理解

运用了分治思想，对每个单元格(cell)独立地进行处理。该技术的基本假设是，一个轮廓只能以有限数量的方式通过一个单元格。我们可以构造一个案例表(case table)，它枚举一个单元的所有可能的拓扑状态（topological state）。拓扑状态的数量取决于单元格顶点的数量，以及一个顶点相对于轮廓值可以具有的内部/外部关系的数量。标量值大于轮廓值的顶点被称为在轮廓之内。标量值小于轮廓值的顶点被称为在轮廓之外。例如，如果一个单元格有四个顶点，并且每个顶点可以在轮廓内部或外部，则有2^4 = 16种可能的方式通过单元格（在实现时可以用bit来实现）。在案例表中，我们不感兴趣的是轮廓通过单元格的位置（例如，geometrical intersection），感兴趣的只是它如何通过单元格（即单元格中轮廓的topology）。

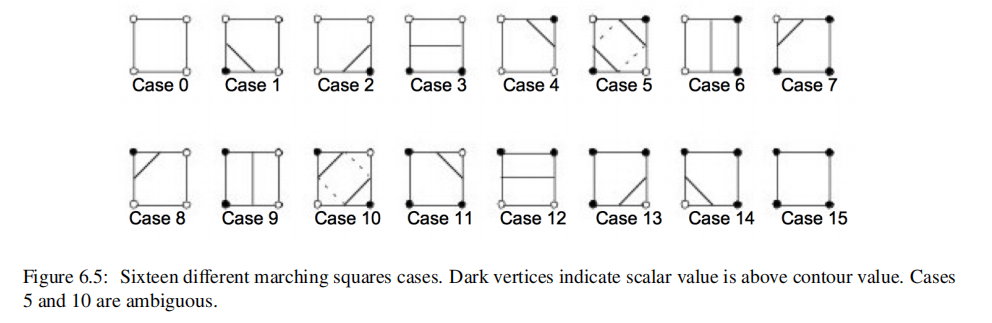
一旦我们选择好属于哪一种case之后，就可以使用插值来计算contour line与cell edge相交的位置。该算法处理一个单元格，然后移动，或行进到下一个单元格。在访问所有单元格后，将完成轮廓。因此称为marching cubes。

算法的步骤如下：

1. Select a cell.

2. Calculate the inside / outside state of each vertex of the cell.

3. Create an index by storing the binary state of each vertex in a separate bit.

4. Use the index to look up the topological state of the cell in a case table.

5. Calculate the contour location (via interpolation) for each edge in the case table.

 

 这个过程将在每个单元格中构造独立的几何原元。在单元格边界处，可以创建重复的顶点和边。这些重复项可以通过使用一个特殊的重合点合并（point merging）操作来消除。请注意，沿着每条边的插值都应该在相同的方向上进行。若不这样，数值舍入很可能导致生成的点不完全一致（not precisely coincident），并且不能正确合并（merge）。这一步骤称为merge coincident points。

 

三、Marching cubes算法——3D情况

对于6面体，有8个顶点，因此有2^8 = 256中情况，又由于对称性，最后只保留15种情况，如下图：

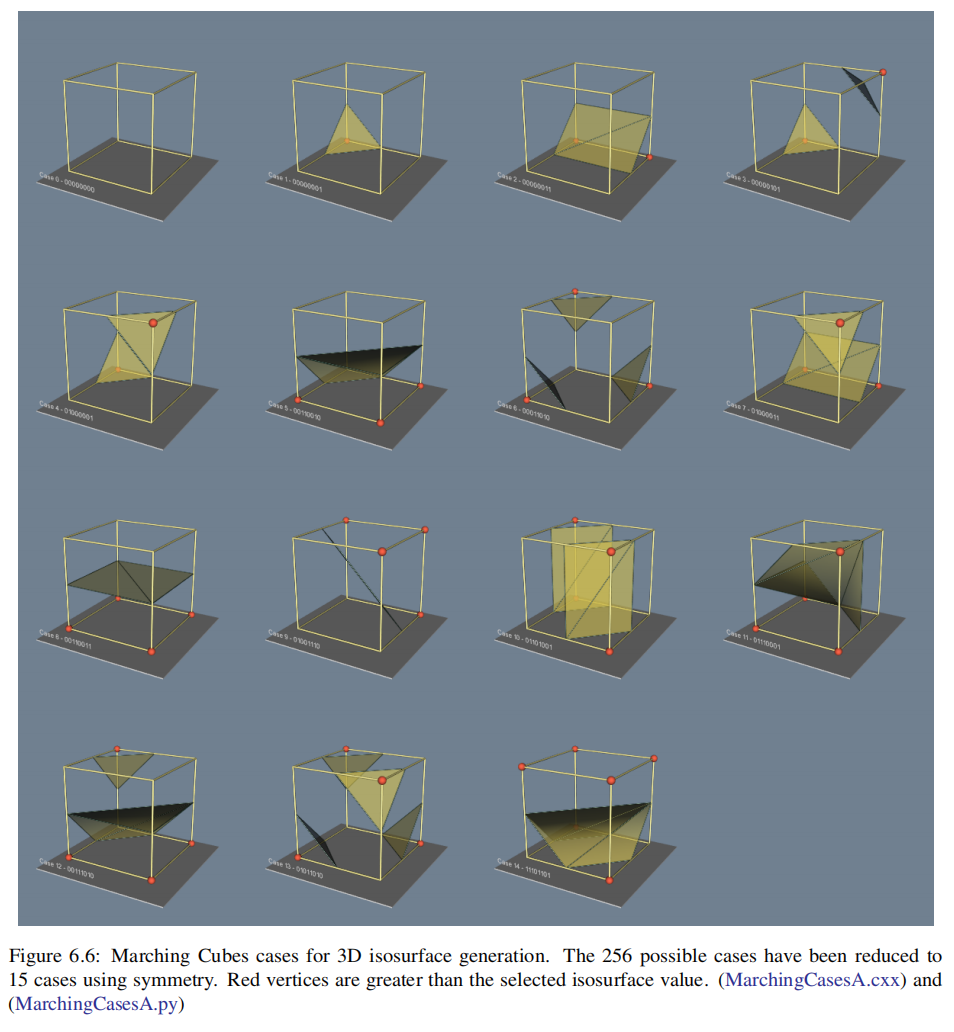
 四、算法需要注意的事项

在2D中，轮廓模糊（ambiguos cases，如Fig6.5中的Case 5和Case 10）很容易处理：对于每个模糊的情况，我们选择实现两种可能的情况中的一种。根据选择的不同，轮廓可以延伸或打破当前的轮廓，如Fig 6.9所示。任何一种选择都是可以接受的，因为产生的等高线（contour line）将是连续的和封闭的（或将在数据集(data set)边界结束）。

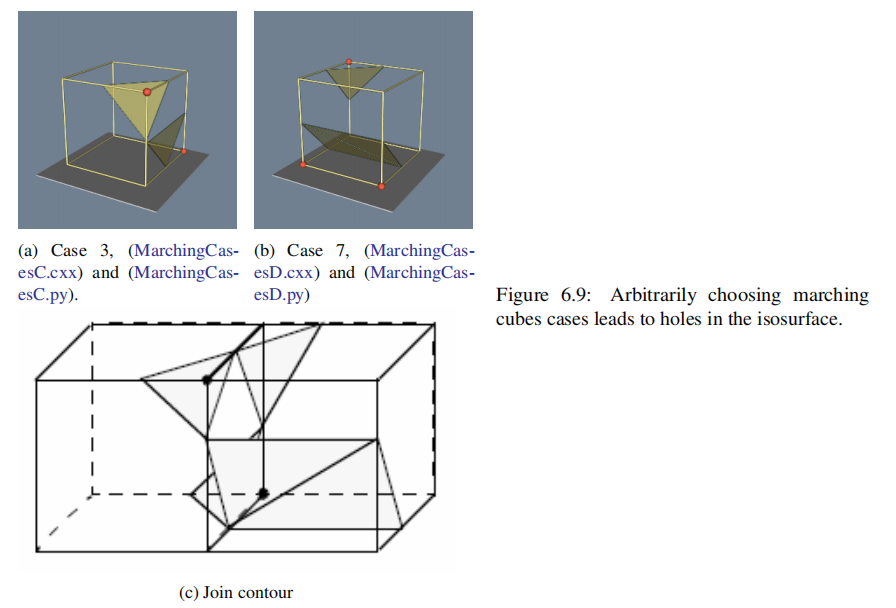
在3D中，这个问题更为复杂。我们不能简单地选择一个独立于所有其他模糊案例的模糊案例。例如，Fig 6.9显示了如果我们不小心实现了两个相互独立的情况，会发生什么。在这个图中，我们使用了通常的情况3，但用它的互补情况替换了情况6。互补的情况是通过将“暗”顶点与“光”顶点交换而形成的。（这相当于将顶点标量值从等值面值以上切换到等值面值以下，反之亦然。）将这两种情况配对的结果是在等值面上留下了一个孔(hole)。

一个简单而有效的解决方案通过添加额外的互补案例(complementary cases)，扩展了原来的15个marching cubes案例。这些情况被设计成与邻近的情况兼容，并防止在等值面上产生孔。需要6个互补的情况，分别对应于行进立方体的情况3、6、7、10、12和13。互补的行进立方体案例如Fig 6.10所示。

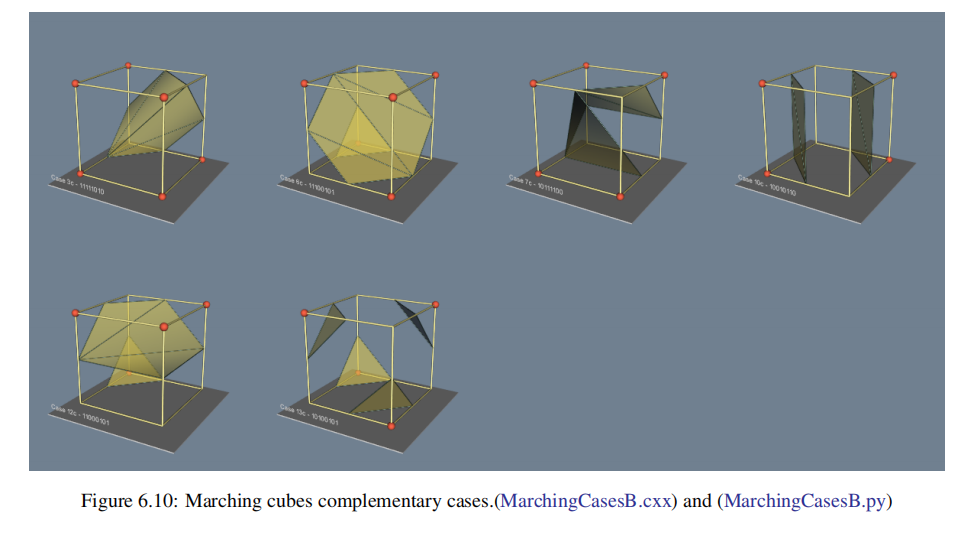
此外，尽管我们说该算法用于规则类型，如四边形和立方体，但marching cubes可以应用于任何拓扑上等同于立方体的单元类型（例如，六面体或非立方体体素）。

五、应用

Fig 6.11d是由marching cubes创建的等值面。图6.11b是一个来自计算机断层扫描（CT）x射线成像系统的恒定图像强度（image intensity）的表面。（图6.11a是该数据的二维子集。）其强度水平对应于人的骨骼。图6.11c为恒定流密度（flow density）的等值面。图6.11d为铁蛋白分子的电子势等值面。由于我们熟悉人体解剖学，图6.11b中所示的图像可以立即被识别出来。然而，对于计算流体动力学和分子生物学领域的从业者来说，图6.11c和图6.11d同样熟悉。正如这些例子所显示的，轮廓形成的方法是各领域可视化数据的强大而又通用的技术。

参考文档：VTKTextBook Scalar Algorithms