【原】Coursera—Andrew Ng机器学习—课程笔记 Lecture 3

Lecture3 Linear Algebra Review 线性代数回顾

3.1 矩阵和向量
3.2 加法和标量乘法
3.3 矩阵向量乘法
3.4 矩阵乘法
3.5 矩阵乘法的性质
3.6 逆、转置

3.1 矩阵和向量　　

　　参考视频: 3 - 1 - Matrices and Vectors (9 min).mkv

3.2 加法和标量乘法

　　参考视频: 3 - 2 - Addition and Scalar Multiplication (7 min).mkv

3.3 矩阵向量乘法

　　参考视频: 3 - 3 - Matrix Vector Multiplication (14 min).mkv

3.4 矩阵乘法

　　参考视频: 3 - 4 - Matrix Matrix Multiplication (11 min).mkv

3.5 矩阵乘法的性质

　　参考视频: 3 - 5 - Matrix Multiplication Properties (9 min).mkv

　　矩阵的乘法有以下规律：

1、不符合交换律 commutative　A × B ≠ B× A　　【但是对于单位矩阵，有AI = IA = A】

　　 2、符合组合律 associative　　 A ×（B× C） =（A × B）× C

3.6 逆、转置

3.6.1 矩阵的逆 Inverse Matrix

　　矩阵的逆 A^-1Inverse Matrix。如矩阵 A 是一个 m× m 矩阵（方阵），如果有逆矩阵A^-1，则：

　　I 称为 单位矩阵 Identity Matrix

　　没有逆矩阵的矩阵称为 奇异矩阵singular matrix 或者 退化矩阵 degenerate matrix。

　　规则：

　　1、只有方阵有逆矩阵。

　　2、零矩阵没有逆矩阵（还有其他一些矩阵没有逆矩阵，可以想成是一些特别接近零矩阵的矩阵）

3.6.2 使用 Octave 计算矩阵的逆

计算矩阵的逆通常使用MATLAB 或者 Octave，打开Octave的bash界面。

　　以下是在Octave里计算逆矩阵的过程：

 Please contribute if you find this software useful.

 For more information, visit https://www.octave.org/get-involved.html

 Read https://www.octave.org/bugs.html to learn how to submit bug reports.

 For information about changes from previous versions, type 'news'.

 octave:> A = [ ;  ]　　　　　　　　　　// 输入一个矩阵 A

 A =

 octave:> pinv(A)　　　　　　　　　　　　　　 // 计算其逆矩阵 InverseOfA

 ans =

    0.400000  -0.100000

   -0.050000   0.075000

 octave:> inverseOfA = pinv(A)

 inverseOfA =

    0.400000  -0.100000

   -0.050000   0.075000

 octave:> A * pinv(A)　　　　　　　　　　

 ans =

    1.0000e+00   5.5511e-17　　　　　　　　 // 由于计算精度的问题， 四舍五入导致次对角线元素不是0，而是10的-17方、10的-16方，可以近似于0

   -2.2204e-16   1.0000e+00

 octave:> A * inverseOfA　　　　　　　　　　// 计算 A * InverseOfA

 ans =

    1.0000e+00   5.5511e-17

   -2.2204e-16   1.0000e+00

 octave:> inverseOfA * A　　　　　　　　　　// 计算 InverseOfA * A 

 ans =

    1.00000  -0.00000

    0.00000   1.00000

 octave:>

3.6.3 矩阵的转置

　　矩阵转置 Transpose Matrix ，符号为A^T。

　　定义：设 A 为 m× n 阶矩阵（即 m 行 n 列），第 i 行 j 列的元素是 a(i,j)，即：A = a(i,j)。定义 A 的转置为这样一个 n× m 阶矩阵 B，满足 B=a(j,i)，即 b (i,j)=a (j,i)（B 的第 i 行第 j 列元素是 A 的第 j 行第 i 列元素），记 AT=B。 (有些书记为 A'=B）
直观来看，将 A 的所有元素绕着一条从第 1 行第 1 列元素出发的右下方 45 度的射线作镜面反转，即得到 A 的转置。

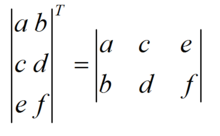
矩阵的转置基本性质：

(A ± B) T = AT ± BT
(A × B) T= BT × AT
(AT) T = A
(KA) T = KAT

　　MATLAB 和 Octave 中矩阵转置：直接打一撇， B = A'。

 octave:> B = A'

 B =

术语

up to the numerical precision 由于计算精度的问题

essentially 根本上

ten to the minus seventeen 10的-17次方

round off 四舍五入

optimal matrices 最优矩阵