【HNOI2008】玩具装箱TOY & 斜率优化学习笔记

题目

P教授要去看奥运，但是他舍不下他的玩具，于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩，其可以将任意物品变成一堆，再放到一种特殊的一维容器中。P教授有编号为 \(1\cdots N\) 的 \(N\) 件玩具，第 \(i\) 件玩具经过压缩后变成一维长度为 \(C_i\) .为了方便整理，P教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物，形式地说如果将第 \(i\) 件玩具到第 \(j\) 个玩具放到一个容器中，那么容器的长度将为 \(x=j-i+\sum\limits_{k=i}^{j}C_k\) 制作容器的费用与容器的长度有关，根据教授研究，如果容器长度为 \(x\) ,其制作费用为 \((x-L)^2\) .其中 \(L\) 是一个常量。P教授不关心容器的数目，他可以制作出任意长度的容器，甚至超过 \(L\) 。但他希望费用最小.

\(0\le n \le 5\times 10^4\)

分析

设 \(f_i\) 代表前 \(i\) 个玩具的最小费用。

显然有：

\[f_i = \min_{j=0}^{i-1} \{f_j + (i - j - 1 + S_i - S_j - L)^2\} = \min_{j=0}^{i-1} \{f_j + (i + S_i - j - S_j - 1 - L)^2\}
\]

其中，\(S_{i} = \sum_{j=0}^i C_j\).

使用换元法，将只与 \(i\) 或 \(j\) 有关的项提取出来。（常数项无所谓）

设 \(A_i = i + S_i\), \(B_i = A_i + L + 1\).

则有：

\[f_i = \min_{j=0}^{i-1} \{f_j + (A_i - B_j)^2\} = \min_{j=0}^{i-1} \{f_j + B_j^2 - 2A_iB_j\} + A_i^2
\]

对于决策 \(j\) ，设：

\[b = f_j + B_j^2 - 2A_iB_j
\]

最优的 \(j\) 就是使 \(b\) 最小的 \(j\).

移项得：

\[f_j + B_j^2 = 2A_iB_j + b
\]

发现这个式子非常眼熟，设 \(k = 2A_i, y = f_j + B_j^2, x = B_j​\).

就变成了直线的解析式：\(y = kx + b​\)

而这个式子中，对于所有的决策，斜率 \(k\) 都是常量，我们需要找到一个 \(j​\) 使得截距最小。

对于每一个决策 \(j\) 都给出了一个点 \(P_j(B_j, f_j + B_j^2)\)，问题就转换成了：已知若干个点和斜率（\(k>0​\)），求过这些点之中一个且斜率为给定值的直线中截距最小的一个。

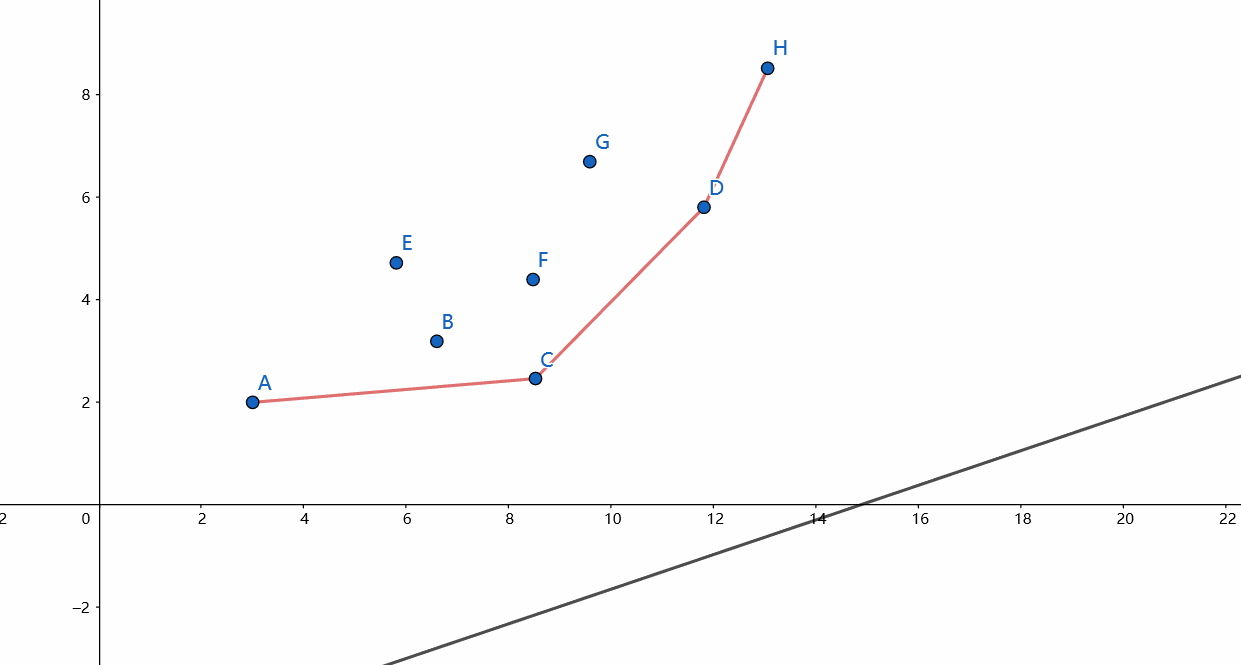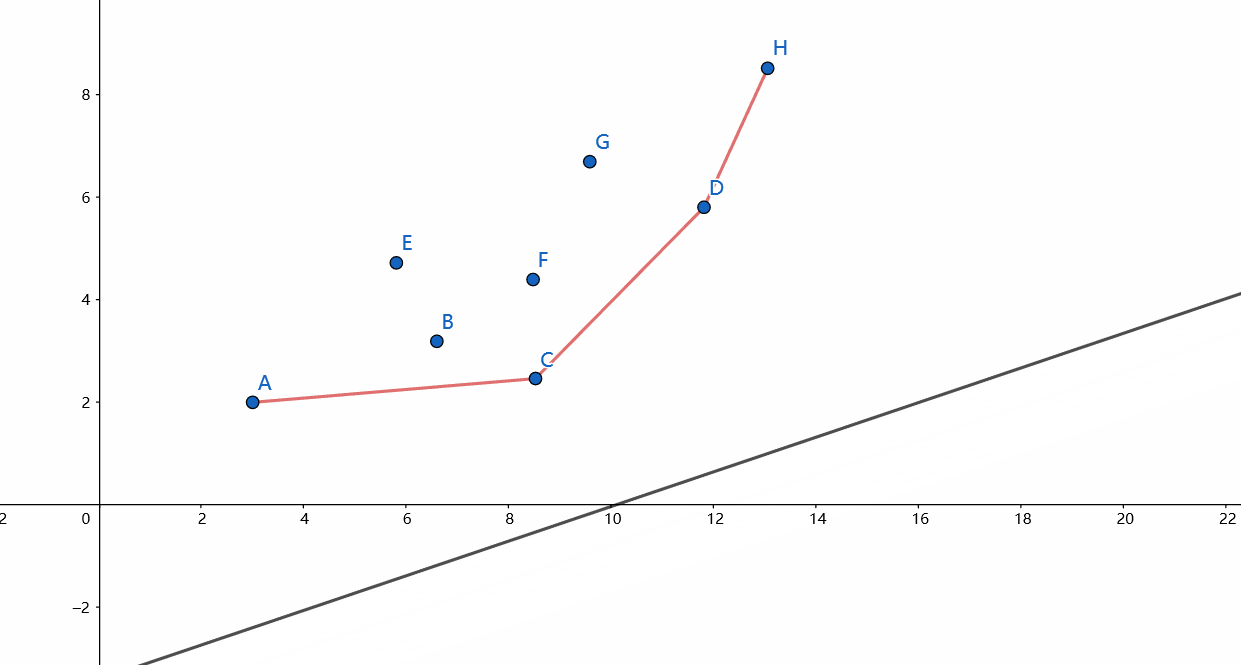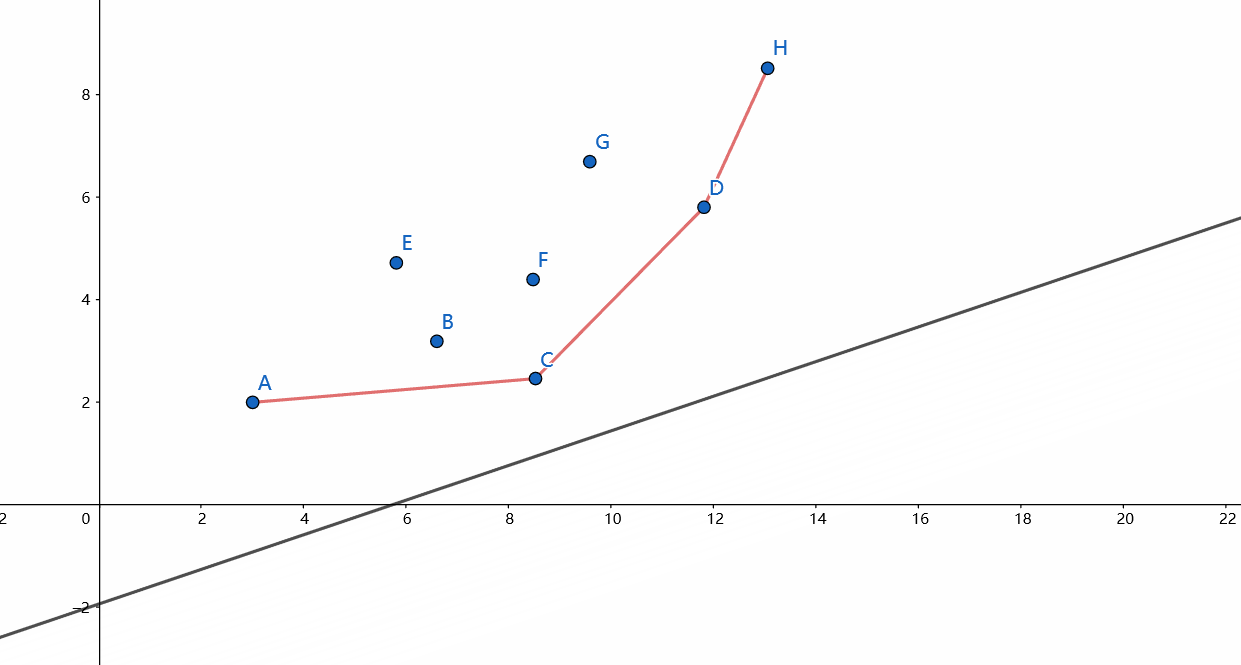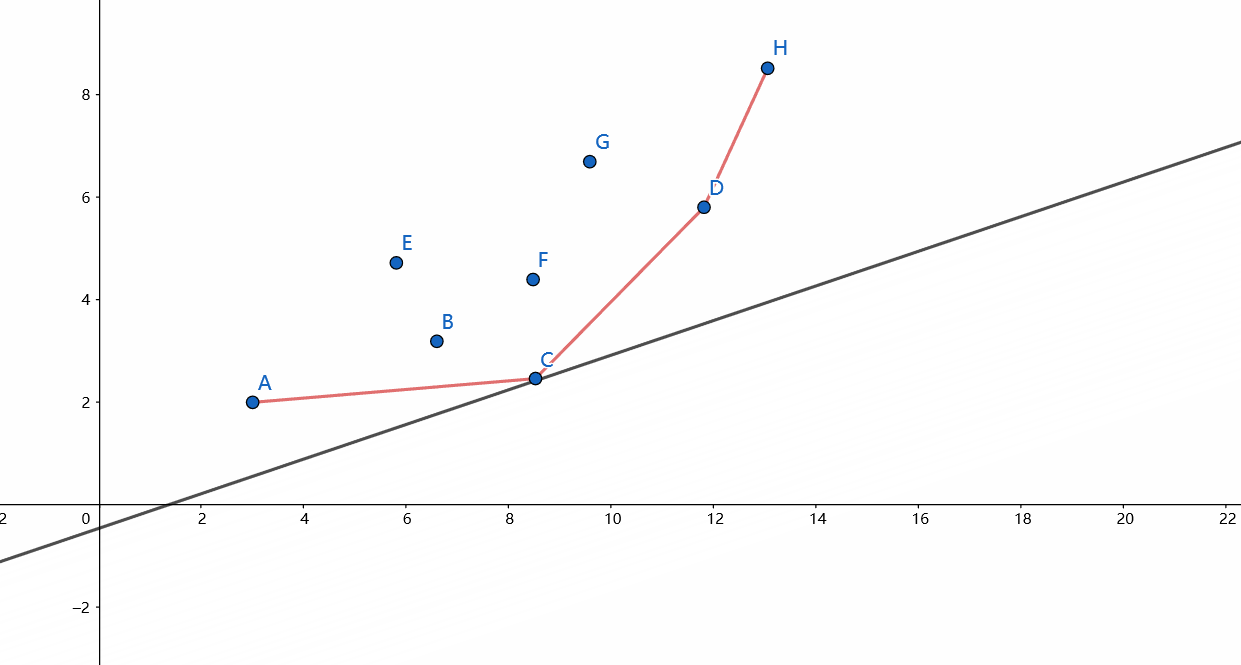
考虑这样一条不断向上移动的直线，当它不断上移时截距越来越大，直到它碰到第一个点为止，这个点就是使截距最小的点。

引理：候选决策连线段的斜率必然递增

证明：\(j​\) 要是 \(i​\) 时最优决策，它必须满足：

\[\forall i>k\not =j\quad f_j + B_j^2 - 2A_iB_j\ < f_k + B_k^2 - 2A_iB_k
\]

即：

\[\begin{align*}
2A_i(B_j + B_k) & < f_k + B_k^2 - f_j - B^2_j \\
2A_i & < \frac{f_k + B_k^2 - (f_j + B^2_j)}{B_j + B_k}
\end{align*}
\]

我们发现，这就是 \(P_jP_i​\) 的斜率 \(> 2A_i​\).

而 \(2A_i​\) 就是我们不断上移的直线的斜率 \(k​\).

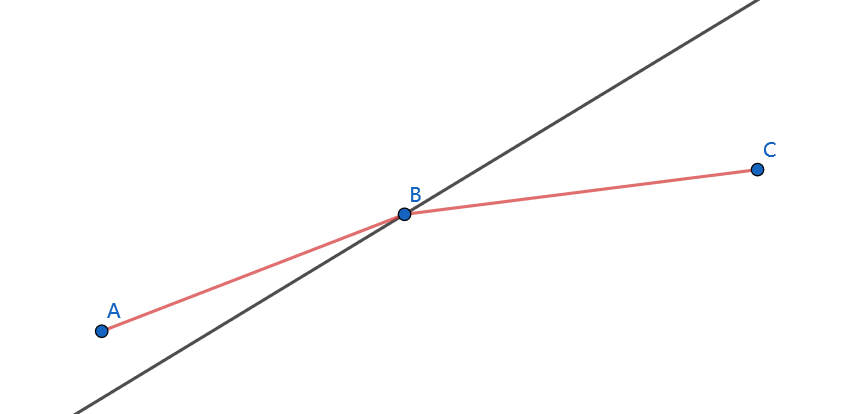
所以，若 \(B\) 可能是最优决策点，则另外一个可能的最优决策点 \(C\) 必然在直线 \(y = kx + b\) 的左侧而非右侧。

所以，最优解一定在决策的下凸壳上。

我们可以轻易的证明 \(A_i​\) 单调递增。

考虑使用一个单调队列维护第一个使得斜率 \(>A_i\) 的点，然后就结束了。

不过，有时候 \(A_i\) 没有单调递增，那就需要Cdq或者平衡树维护了，那就是下篇的事了。

代码

#include <bits/stdc++.h>

typedef long long ll;

const double eps = 1e-7;
const int kMaxN = 5e5 + 5;

ll S[kMaxN], f[kMaxN], C[kMaxN], n, L;
std::deque<int> que;

ll A(int i) {return i + S[i];}
ll B(int i) {return A(i) + L + 1;}
ll PointX(int i) {return B(i);}
ll PointY(int i) {return f[i] + B(i) * B(i);}
double Slope(int i, int j) {
	return (PointY(i) - PointY(j)) / (double)(PointX(i) - PointX(j));
}

int main() {
	scanf("%lld%lld", &n, &L);
	for(int i = 1; i <= n; i++) {
		scanf("%lld", C + i);
		S[i] = S[i - 1] + C[i];
	}
	f[0] = 0;
	que.push_back(0);
	for(int i = 1; i <= n; i++) {
		while(que.size() > 1 && Slope(que.front(), que[1]) < 2 * A(i))
			que.pop_front();
		int tmp = que.front();
		f[i] = f[tmp] + (A(i) - B(tmp)) * (A(i) - B(tmp));
		while(
			que.size() > 1 &&
			Slope(que.back(), i) < Slope(que.back(), que[que.size() - 2])
		)
			que.pop_back();
		que.push_back(i);
	}
	printf("%lld", f[n]);
	return 0;
}