洛谷P1273 有线电视网 (树上分组背包)

洛谷P1273 有线电视网

题目描述

某收费有线电视网计划转播一场重要的足球比赛。他们的转播网和用户终端构成一棵树状结构，这棵树的根结点位于足球比赛的现场，树叶为各个用户终端，其他中转站为该树的内部节点。

从转播站到转播站以及从转播站到所有用户终端的信号传输费用都是已知的，一场转播的总费用等于传输信号的费用总和。

现在每个用户都准备了一笔费用想观看这场精彩的足球比赛，有线电视网有权决定给哪些用户提供信号而不给哪些用户提供信号。

写一个程序找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。

输入输出格式

输入格式：

输入文件的第一行包含两个用空格隔开的整数N和M，其中2≤N≤3000，1≤M≤N-1，N为整个有线电视网的结点总数，M为用户终端的数量。

第一个转播站即树的根结点编号为1，其他的转播站编号为2到N-M，用户终端编号为N-M+1到N。

接下来的N-M行每行表示—个转播站的数据，第i+1行表示第i个转播站的数据，其格式如下：

K A1 C1 A2 C2 … Ak Ck

K表示该转播站下接K个结点(转播站或用户)，每个结点对应一对整数A与C，A表示结点编号，C表示从当前转播站传输信号到结点A的费用。最后一行依次表示所有用户为观看比赛而准备支付的钱数。

输出格式：

输出文件仅一行，包含一个整数，表示上述问题所要求的最大用户数。

输入输出样例

输入样例#1：

5 3

2 2 2 5 3

2 3 2 4 3

3 4 2

输出样例#1：

2

说明

样例解释

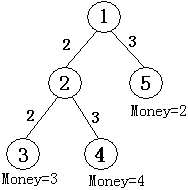
如图所示，共有五个结点。结点①为根结点，即现场直播站，②为一个中转站，③④⑤为用户端，共M个，编号从N-M+1到N，他们为观看比赛分别准备的钱数为3、4、2，从结点①可以传送信号到结点②，费用为2，也可以传送信号到结点⑤，费用为3（第二行数据所示），从结点②可以传输信号到结点③，费用为2。也可传输信号到结点④，费用为3（第三行数据所示），如果要让所有用户（③④⑤）都能看上比赛，则信号传输的总费用为：

2+3+2+3=10，大于用户愿意支付的总费用3+4+2=9，有线电视网就亏本了，而只让③④两个用户看比赛就不亏本了。

Solution

首先,树形结构,应该可以看出来吧

其次,题目中给了我们一个条件,就是收取的费用一定要大于等于建造的费用

所以可以看做是一个背包

树上背包!!!

具体是什么背包呢?

我们把每个节点所选的用户数看成一个个元素,比如选一个用户是一个元素,选两个用户也是一个元素,其中这些元素是互斥的,熟悉背包的同学应该已经看出来了

分组背包:有若干组物品,其中每组物品都只能选一个

那么在这道题中,容量就是以一个节点为根的子树的节点数,组数就是子节点的个数,我们要做的就是枚举每一组中的元素选择多少个客户

设\(dp[i][j]\)为以i为根的子树中选择j个客户的花费

目标状态:\(max(i),dp[1][i]>=0\)

怎么转移?

\[dp[u][j]=max(dp[u][j],dp[u][j-k]+dp[v][k]-w)
\]

解释一下,其中v是u的子节点,w是\(u\to v\)的花费,j和k都是枚举的选择客户的个数,但j的范围是u的整个子树的节点数,k是子节点的子树的节点数

边界

memset(dp,~0x3f,sizeof(dp));
for(rg int i=1;i<=n;i++) dp[i][0]=0;//每个节点都不选,花费当然是0

Code

#include<bits/stdc++.h>
#define in(i) (i=read())
#define rg register
#define il extern inline
using namespace std;

const int N=3e3+10;

int read() {
	int ans=0,f=1; char i=getchar();
	while(i<'0' || i>'9') {if(i=='-') f=-1; i=getchar();}
	while(i>='0' && i<='9') ans=ans*10+(i^48),i=getchar();
	return ans*f;
}

int n,m,cur;
int to[N],nex[N],head[N],w[N];
int dp[N][N],v[N];
il void add(int a,int b,int c) {
	to[++cur]=b,nex[cur]=head[a];
	w[cur]=c,head[a]=cur;
}
int dfs(int u,int sum=0) {
	if(u>=n-m+1) {
		dp[u][1]=v[u];
		return 1;
	}
	for(rg int i=head[u];i;i=nex[i]) {
		int t=dfs(to[i]);sum+=t;
		for(rg int j=sum;j>=1;j--) {
			for(rg int k=1;k<=t;k++) {
				if(j-k>=0) dp[u][j]=max(dp[u][j],dp[u][j-k]+dp[to[i]][k]-w[i]);
			}
		}
	}return sum;
}
int main()
{
	in(n),in(m); memset(dp,~0x3f,sizeof(dp));
	for(rg int i=1;i<=n-m;i++) {
		int k,a,b; in(k);
		for(rg int j=1;j<=k;j++)
			in(a),in(b),add(i,a,b);
	}
	for(rg int i=n-m+1;i<=n;i++) in(v[i]);
	for(rg int i=1;i<=n;i++) dp[i][0]=0;
	dfs(1);
	for(rg int i=m;i>=1;i--)
	if(dp[1][i]>=0) cout<<i<<endl,exit(0);
}

博主蒟蒻,随意转载.但必须附上原文链接

http://www.cnblogs.com/real-l/