Luogu P1801 黑匣子_NOI导刊2010提高（06）

P1801 黑匣子_NOI导刊2010提高（06）

题目描述

Black Box是一种原始的数据库。它可以储存一个整数数组，还有一个特别的变量i。最开始的时候Black Box是空的．而i等于0。这个Black Box要处理一串命令。

命令只有两种：

ADD(x):把x元素放进BlackBox;

GET:i加1，然后输出Blackhox中第i小的数。

记住：第i小的数，就是Black Box里的数的按从小到大的顺序排序后的第i个元素。例如：

我们来演示一下一个有11个命令的命令串。（如下图所示）

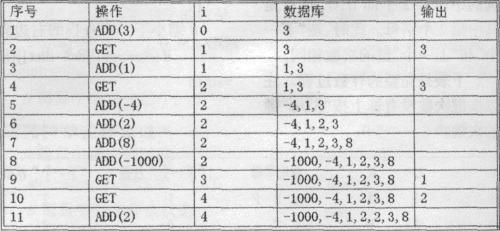
现在要求找出对于给定的命令串的最好的处理方法。ADD和GET命令分别最多200000个。现在用两个整数数组来表示命令串：

1.A(1)，A(2)，…A(M)：一串将要被放进Black Box的元素。每个数都是绝对值不超过2000000000的整数，M$200000。例如上面的例子就是A=(3，1，一4，2，8，-1000，2)。

2.u(1)，u(2)，…u(N)：表示第u(j)个元素被放进了Black Box里后就出现一个GET命令。例如上面的例子中u=(l，2，6，6)。输入数据不用判错。

输入输出格式

输入格式：

第一行，两个整数，M，N。

第二行，M个整数，表示A(l)

……A(M)。

第三行，N个整数，表示u(l)

…u(N)。

输出格式：

输出Black Box根据命令串所得出的输出串，一个数字一行。

输入输出样例

输入样例#1： 复制

7 4
3 1 -4 2 8 -1000 2
1 2 6 6

输出样例#1： 复制

3
3
1
2

说明

对于30%的数据，M≤10000;

对于50%的数据，M≤100000：

对于100%的数据，M≤200000。

 #include<cstdio>
 //#include<iostream>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 #include<queue>
 #define INF 0x3f3f3f3f
 #define N 100005
 #define re register
 #define Ii inline int
 #define Il inline long long
 #define Iv inline void
 #define Ib inline bool
 #define Id inline double
 #define ll long long
 #define Fill(a,b) memset(a,b,sizeof(a))
 #define R(a,b,c) for(register int a=b;a<=c;++a)
 #define nR(a,b,c) for(register int a=b;a>=c;--a)
 #define Min(a,b) ((a)<(b)?(a):(b))
 #define Max(a,b) ((a)>(b)?(a):(b))
 #define Cmin(a,b) ((a)=(a)<(b)?(a):(b))
 #define Cmax(a,b) ((a)=(a)>(b)?(a):(b))
 #define D_e(x) printf("&__ %d __&\n",x)
 #define D_e_Line printf("-----------------\n")
 using namespace std;
 Ii read(){
     int s=,f=;char c;
     for(c=getchar();c>''||c<'';c=getchar())if(c=='-')f=-;
     while(c>=''&&c<='')s=s*+(c^''),c=getchar();
     return s*f;
 }
 Iv print(int x){
     if(x<)putchar('-'),x=-x;
     if(x>)print(x/);
     putchar(x%^'');
 }
 priority_queue<int>q_box;
 priority_queue<int,vector<int>,greater<int> >q_ans;
 int add[],get[];
 int main(){
     int m=read(),n=read();
     R(i,,m)
         add[i]=read();
     R(i,,n)
         get[i]=read();
     int cnt=;
     R(i,,n){
         while(cnt<get[i])
             ++cnt,
             q_box.push(add[cnt]),
             q_ans.push(q_box.top()),
             q_box.pop();
         print(q_ans.top()),putchar('\n'),
         q_box.push(q_ans.top()),
         q_ans.pop();
     }
     return ;
 }