图的遍历——DFS

原创

---

图的遍历有DFS和BFS两种，现选用DFS遍历图。

存储图用邻接矩阵，图有v个顶点，e条边，邻接矩阵就是一个VxV的矩阵；

若顶点1和顶点5之间有连线，则矩阵元素[1,5]置1，若是无向图[5,1]也

置1，两顶点之间无连线则置无穷，顶点到顶点本身置0。

例如：

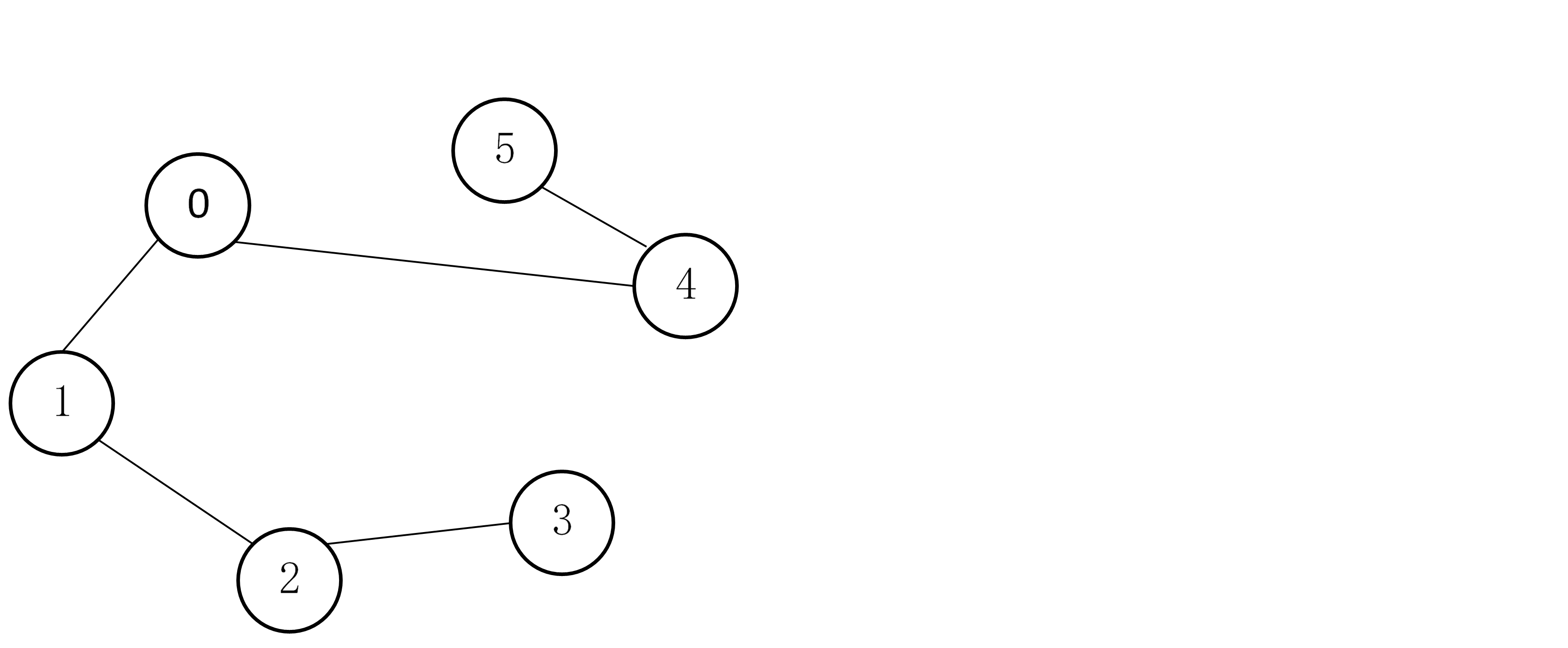
邻接矩阵为：

遍历思路：

　　随便选择一未访问过的顶点v1作为遍历起点，访问v1，再选择与v1连接的点v2作为起始点，访问v2；

再选择与v2连接的点作为起始点v3，访问v3，假设v3是孤立点，则v3不能往下访问，回溯到v2，再以v2

作为起点，访问与v2连接的其他未被访问过的顶点，假设是v4，则再以v4为顶点，访问v4，再选择与v4

连接的顶点为起始点......直到全部顶点都被访问过一遍。

　　在上图中，假设以顶点2为起点进行图的遍历，则先访问顶点2，再访问顶点1，注意，并不是先访问

3，因为在扫描邻接矩阵时，在每行是从左向右扫描的；再访问顶点0，再深搜下去访问顶点4，访问顶点

5，一直回溯，回溯到顶点2，再访问顶点3；访问顺序为：2 1 0 4 5 3 

Java：

import java.util.*;

public class 图的遍历_dfs {

    static int v;    //顶点数
    static int e;    //边数
    static int arr[][];
    static int book[];    //标识顶点是否访问
    static int max=99999;    //无穷
    static int total=0;    //统计已访问顶点个数

    static void graph_dfs(int ver) {    //ver表示顶点
        total++;
        book[ver]=1;    //标记顶点ver已经访问过
        System.out.print(ver+" ");
        if(total==v) {
            return;
        }
        for(int i=0;i<v;i++) {
            if(arr[ver][i]==1 && book[i]==0) {
                graph_dfs(i);
            }
        }
        return;
    }

    public static void main(String[] args) {
        Scanner reader=new Scanner(System.in);
        v=reader.nextInt();
        e=reader.nextInt();
        arr=new int[v][v];
        book=new int[v];
        //邻接矩阵初始化
        for(int i=0;i<v;i++) {
            book[i]=0;
            for(int j=0;j<v;j++) {
                if(i==j) {
                    arr[i][j]=0;
                }
                else {
                    arr[i][j]=max;
                }
            }
        }
        //读入边
        for(int i=0;i<e;i++) {
            int first_E=reader.nextInt();
            int second_E=reader.nextInt();
            arr[first_E][second_E]=1;
            arr[second_E][first_E]=1;
        }
        graph_dfs(0);    //从顶点0开始遍历
    }

}

18:08:52

2018-07-22