接下来准备写支持向量机，然而支持向量机和其他算法相比牵涉较多的数学知识，其中首当其冲的就是标题中的拉格朗日乘子法、KKT条件和对偶问题，所以本篇先作个铺垫。

大部分机器学习算法最后都可归结为最优化问题。对于无约束优化问题： \(\min\limits_\boldsymbol{x} f(\boldsymbol{x})\) (本篇为形式统一，只考虑极小化问题)，一般可直接求导并用梯度下降或牛顿法迭代求得最优值。

对于含有等式约束的优化问题，即：
\[
\begin{aligned}
{\min_{\boldsymbol{x}}} & \;\;{f(\boldsymbol{x})} \\ {\text { s.t. }} & \;\;{h_{i}(\boldsymbol{x}) = 0}, \quad i=1,2, \ldots, m
\end{aligned}
\]
由于等式约束 \(h_i(\boldsymbol{x}) = 0\) 的存在，无法直接求导迭代求解。拉格朗日乘子法是解决此类问题的常用方法，其核心思想是将约束优化转化为无约束优化问题，即将有 \(d\) 个变量和 \(m\) 个等式约束条件的最优化问题转换为一个有 \((d + m)\) 个变量的函数求平稳点的问题。

拉格朗日乘子法

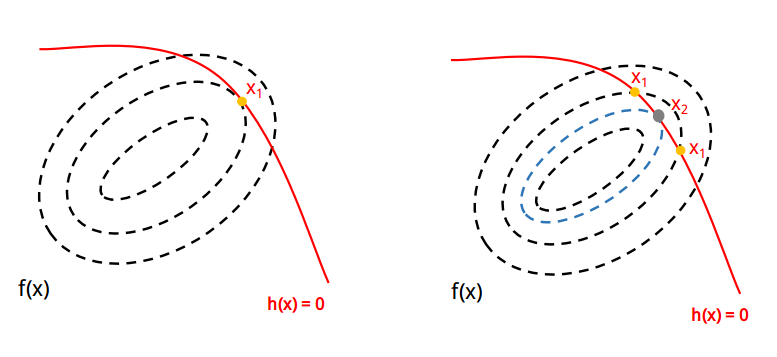
下面画图来直观理解拉格朗日乘子法，先看下左图：黑色虚线为函数 \(f(x)\) 的等值线，红色实线为约束条件 \(h(x) = 0\) ，这里的关键是 \(f(x)\) 在极小点处必然与 \(h(x) = 0\) 相切，如下左图相切于黄色点 \(x_1\) 。为什么这么说？来看下右图：如果 \(f(x)\) 与 \(h(x) = 0\) 不相切，则相交于两个黄色点，而由于 \(x\) 是连续的，则必然能找到一个新的 \(x_2\) 使得 \(f(x_2)\) 更小，图中表示为蓝色虚线，使得在 \(x_2\) 处 \(f(x)\) 与 \(h(x) = 0\) 相切。

由于相交的两个黄色点不是极小点，梯度 \(\nabla f(x_1)\) 仍然会沿着 \(h(x) = 0\) 变化，因而在这两个点 \(\nabla f(x_1)\) 不与 \(h(x) = 0\) 的切线方向垂直，只有在极小点才会正交。

由此可以得出两个推论 (见下图)：

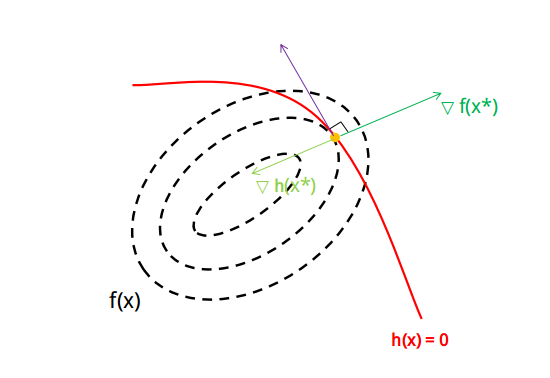
(1). 对于 \(f(\boldsymbol{x})\) 的极小点 \(\boldsymbol{x}^*\) ，\(f(\boldsymbol{x})\) 在 \(\boldsymbol{x}^*\) 处的梯度 \(\nabla f(\boldsymbol{x}^*)\) 与 \(h(\boldsymbol{x}) = 0\) 的切线方向垂直

(2). 对于 \(f(\boldsymbol{x})\) 的极小点 \(\boldsymbol{x}^*\) ，\(h(\boldsymbol{x})\) 在 \(\boldsymbol{x}^*\) 处的梯度 \(\nabla h(\boldsymbol{x}^*)\) 与 \(h(\boldsymbol{x}) = 0\) 的切线方向垂直

对于第 (2) 点，可作如下证明：设 \(\boldsymbol{x}(t)\) 为连续可微的函数，则有 \(h(\boldsymbol{x}(t)) = 0\) ，利用链式法则：
\[
\frac{\text{d}}{\text{d} t} h(\boldsymbol{x}(t)) = \nabla h(\boldsymbol{x}(t)) \cdot \frac{\text{d}{\boldsymbol{x}(t)}}{\text{d}t} = 0
\]
\(\frac{\text{d}{\boldsymbol{x}(t)}}{\text{d}t}\) 即为切线方向，所以本质上 \(h(\boldsymbol{x}) = 0\) 上任意一点的梯度 \(\nabla h(\boldsymbol{x})\) 都与其正交，\(\boldsymbol{x}^*\) 自然也不例外。

于是可以得出在极小点处 \(\nabla h(\boldsymbol{x}^*)\) 与 \(\nabla f(\boldsymbol{x}^*)\) 平行，即存在 \(\lambda \neq 0\) ，使得：
\[
\nabla f(\boldsymbol{x}^*) + \lambda \nabla h(\boldsymbol{x}^*) = 0 \tag{1.1}
\]
\(\lambda\) 被称为拉格朗日乘子，下面定义拉格朗日函数：
\[
\mathcal{L}(\boldsymbol{x}, \lambda) = f(\boldsymbol{x}) + \lambda \,h(\boldsymbol{x}) \tag{1.2}
\]
将上式分别对 \(\boldsymbol{x}\) 和 \(\lambda\) 求导置零，就分别得到 \((1.1)\) 式和等式约束 \(h(\boldsymbol{x}) = 0\) ，这样就将原约束优化问题转化为对 \(\mathcal{L}(\boldsymbol{x}, \lambda)\) 的无约束优化问题。然而这个方法找出来的平稳点不一定都是原问题的极值点，如下左图是一个极值点，而下右图却不是极值点。

KKT 条件

上面拉格朗日乘子法解决的是等式约束优化问题，而对于不等式约束优化问题也可解，只不过要加一些附加条件：
\[
\begin{aligned}
{\min_{\boldsymbol{x}}} & \;\;{f(\boldsymbol{x})}
\\ {\text { s.t. }} & \;\;{g_{i}(\boldsymbol{x}) \leqslant 0}, \quad i=1,2, \ldots, m
\\ & \;\;{h_{j}(\boldsymbol{x}) = 0}, \quad j=1,2, \ldots, n
\end{aligned}
\]
先下一个定义：

对于一个不等式约束 \(g_j(\boldsymbol{x}) \leqslant 0\) ，若在 \(\boldsymbol{x}^*\) 处 \(g_j(\boldsymbol{x}^*) < 0\) ，那么称该不等式约束是 \(\boldsymbol{x}^*\) 处的不起作用约束；若在 \(\boldsymbol{x}^*\) 处 \(g_j(\boldsymbol{x}^*) = 0\) ，那么称该约束是 \(\boldsymbol{x}^*\) 处的起作用约束。

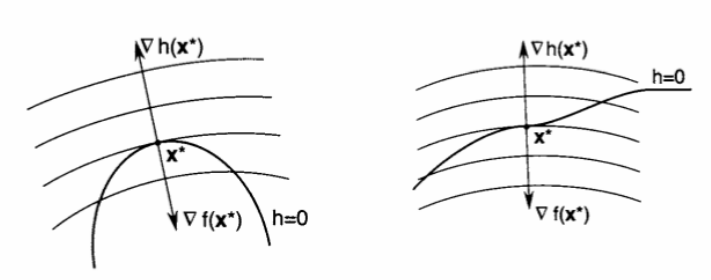
对于该定义的直观解释见下图：灰色部分为约束 \(g(\boldsymbol{x}) \leqslant 0\) 的可行域，若最优点 \(\boldsymbol{x}^*\) 在区域内 (下左图，\(g(\boldsymbol{x}) < 0\) ) ，则约束并没有起到”约束的作用“，这样可直接通过 \(\nabla f(\boldsymbol{x}) = 0\) 来获得最优点，这等价于让 \((1.1)\) 式中 \(\lambda = 0\) 。

若最优点 \(\boldsymbol{x}^*\) 在区域边界上 (下右图，\(g(\boldsymbol{x}) = 0\) ) ，那么对于 \(f(\boldsymbol{x})\) 来说，在 \(\boldsymbol{x}^*\) 处是外部较大，内部较小，因为越靠近等值线中心 \(f(\boldsymbol{x})\) 越小；而对于 \(g(\boldsymbol{x})\) 来说，在 \(\boldsymbol{x}\) 处的变化趋势是内部较小，外部较大，因为在内部 \(g(\boldsymbol{x}) \leqslant 0\) ，外部 \(g(\boldsymbol{x}) > 0\) 。这样 \(\nabla f(\boldsymbol{x}^*)\) 和 \(\nabla g(\boldsymbol{x}^*)\) 的方向必相反，此时 \(g(\boldsymbol{x}) = 0\)，那么套用 \((1.1)\) 式可得 \(\lambda > 0\) 。

综合这两种情况：
\[
\begin{cases} g(\boldsymbol{x}) < 0, & \lambda = 0
\\[1ex] g(\boldsymbol{x}) = 0, & \lambda > 0 \end{cases} \quad \Longrightarrow \quad \lambda \geqslant 0, \;\;\lambda \,g(\boldsymbol{x}) = 0 \tag{2.1}
\]
这被称为互补松弛条件 (\(\text{complementary slackness}\)) 。

由此推广到多个约束，定义广义拉格朗日函数：
\[
\mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) :=f(\boldsymbol{x})+\sum_{i=1}^{m} \alpha_{i} g_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \beta_{j} h_{j}(\boldsymbol{x}) \tag{2.2}
\]
\(\boldsymbol{\alpha} \geqslant 0\) 为 KKT 乘子，\(\boldsymbol{\beta}\) 为拉格朗日乘子，其最优解满足：
\[
\begin{cases}
g_i(\boldsymbol{x}) \leqslant 0, & i=1,2, \ldots, m \qquad\qquad(1) \\[1ex]
{h_{j}(\boldsymbol{x}) = 0}, & j=1,2, \ldots, n \,\qquad\qquad(2) \\[1ex]
\alpha_i \geqslant 0, & i=1,2, \ldots, m \qquad\qquad(3) \\[1ex]
\alpha_i g_i(\boldsymbol{x}) = 0, & i=1,2, \ldots, m \qquad\qquad(4)
\end{cases}
\]
\((1) \sim (2)\) 式为原问题的约束条件，\((3) \sim (4)\) 式上文定义中已证明。这就是不等式约束优化问题的 KKT 条件 (\(\text{Karush-Kuhn-Tucker Condition}\))，KKT 条件是拉格朗日乘子法在不等式约束优化问题上的泛化。KKT 条件是极小点的必要条件，即满足 KKT 条件不一定是极小点，但极小点必满足 KKT 条件。

对偶问题

将原始问题转化为对偶问题是求解带约束优化问题的一种方法，当然这不是唯一的方法，只不过转化为对偶问题后往往更容易求解，因而被广为应用。

设原始优化问题为：
\[
\begin{aligned}
{\min_{\boldsymbol{x}}} & \;\;{f(\boldsymbol{x})}
\\ {\text { s.t. }} & \;\;{g_{i}(\boldsymbol{x}) \leqslant 0}, \quad i=1,2, \ldots, m
\\ & \;\;{h_{j}(\boldsymbol{x}) = 0}, \quad j=1,2, \ldots, n
\end{aligned} \tag{3.1}
\]
其拉格朗日函数为 \(\mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) =f(\boldsymbol{x})+\sum_{i=1}^{m} \alpha_{i} g_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \beta_{j} h_{j}(\boldsymbol{x}), \;\;\alpha \geqslant 0\) 。若 \(\boldsymbol{x}\) 违反了一些约束 (即存在 \(i,j\) 使得 \({g_{i}(\boldsymbol{x}) \geqslant 0}\) 或 \(h_j(\boldsymbol{x}) \neq 0\) ) ，那么 \(\max\limits_{\boldsymbol{\alpha}, \boldsymbol{\beta}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) = \infty\) ，则：
\[
\begin{aligned} \min _{\boldsymbol{x}} \max _{\boldsymbol{\alpha}, \boldsymbol{\beta}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) = & \min _{\boldsymbol{x}}\left(f(\boldsymbol{x})+\max _{\boldsymbol{\alpha}, \boldsymbol{\beta}}\left(\sum_{i=1}^{m} \alpha_{i} g_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \beta_{j} h_{j}(\boldsymbol{x})\right)\right) \\[1ex]
= & \min_{\boldsymbol{x}}\left(f(\boldsymbol{x})+\left\{\begin{array}{l}{0}\,, & 若 \boldsymbol{x} \,满足约束 \\ {\infty}\,, & 若 \boldsymbol{x} \,不满足约束\end{array}\right.\right) \\[1ex]
= & \min_{\boldsymbol{x}} f(\boldsymbol{x}), \;\;且 \boldsymbol{x} \, 满足约束
\end{aligned}
\]
这样原始优化问题 \((3.1)\) 就等价于：
\[
\begin{align*}
\min _{\boldsymbol{x}} \max _{\boldsymbol{\alpha}, \boldsymbol{\beta}} & \;\; \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) \\
\text{s.t.} & \;\; \alpha_i \geqslant 0, \quad i=1,2, \ldots, m
\end{align*}
\]

接下来定义 \((3.1)\) 式的对偶问题 (dual problem) 为：
\[
\begin{align*}
\max _{\boldsymbol{\alpha}, \boldsymbol{\beta}}\min _{\boldsymbol{x}} & \;\; \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) \\
\text{s.t.} & \;\; \alpha_i \geqslant 0, \quad i=1,2, \ldots, m
\end{align*}
\]
对偶问题是原始问题的下界，即：
\[
\max _{\boldsymbol{\alpha}, \boldsymbol{\beta}}\min _{\boldsymbol{x}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) \; \leq \; \min _{\boldsymbol{x}} \max _{\boldsymbol{\alpha}, \boldsymbol{\beta}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) \tag{3.2}
\]
上式为什么成立？因为任意值小于等于最大值，所以对于任意 \(\boldsymbol{\alpha}, \,\boldsymbol{\beta}\) ，\(\min _{\boldsymbol{x}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) \; \leq \; \min _{\boldsymbol{x}} \max _{\boldsymbol{\alpha}, \boldsymbol{\beta}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta})\) ，如果上式恒成立，则不等式左边的 \(\min _{\boldsymbol{x}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta})\) 的极大值 \(\max _{\boldsymbol{\alpha}, \boldsymbol{\beta}}\min _{\boldsymbol{x}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta})\) 一定小于等于不等式右边的 \(\min _{\boldsymbol{x}} \max _{\boldsymbol{\alpha}, \boldsymbol{\beta}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta})\) ，这就是所谓的 ”极小的极大 \(\leqslant\) 极大的极小“ 。

\((3.2)\) 式是不等式，所以该性质被称为弱对偶性 (weak duality)。若要等式成立，则为强对偶性 (strong duality)，需要满足 slater 条件：

\(\text{slater}\) 条件：原始问题为凸优化问题，即 \(f(\boldsymbol{x})\)，\(g(\boldsymbol{x})\) 为凸函数，\(h(\boldsymbol{x})\) 为仿射函数，且可行域中至少有一点使不等式约束严格成立时，强对偶性成立，对偶问题等价于原始问题。

最后，利用强对偶性求出的 \(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}\) 同时也是原始问题的最优解，所以依然满足 KKT 条件：

\[
\begin{cases}
原始问题可行: & g_i(\boldsymbol{x}) \leqslant 0, \;{h_{j}(\boldsymbol{x}) = 0} \\[1ex]
对偶问题可行: & \alpha_i \geqslant 0 \\[1ex]
互补松弛: & \alpha_i g_i(\boldsymbol{x}) = 0 \\[1ex]
拉格朗日平稳性: & \nabla_{\boldsymbol{x}}\mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) = 0
\end{cases}
\]