poj 1852 ants 题解《挑战程序设计竞赛》

地址  http://poj.org/problem?id=1852

题目描述

Description

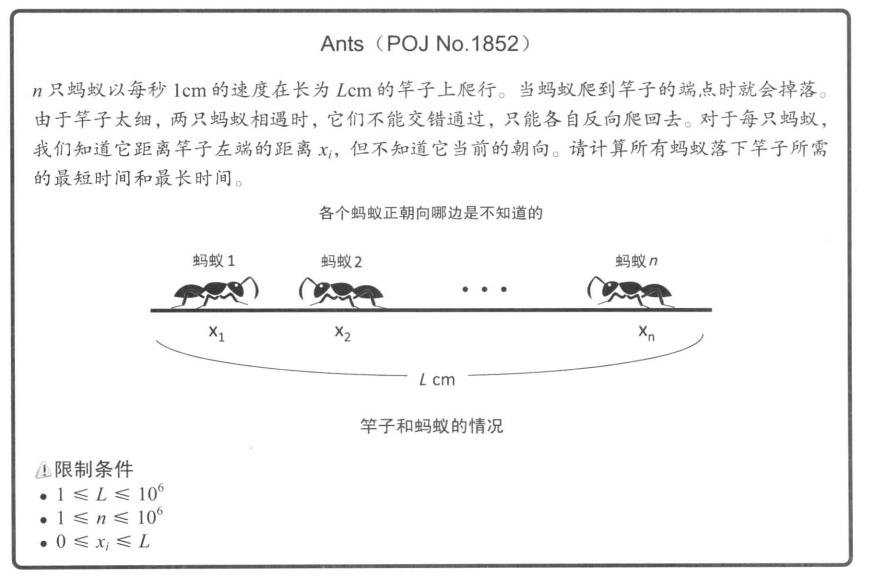
An army of ants walk on a horizontal pole of length l cm, each with a constant speed of 1 cm/s. When a walking ant reaches an end of the pole, it immediatelly falls off it. When two ants meet they turn back and start walking in opposite directions. We know the original positions of ants on the pole, unfortunately, we do not know the directions in which the ants are walking. Your task is to compute the earliest and the latest possible times needed for all ants to fall off the pole.
Input

The first line of input contains one integer giving the number of cases that follow. The data for each case start with two integer numbers: the length of the pole (in cm) and n, the number of ants residing on the pole. These two numbers are followed by n integers giving the position of each ant on the pole as the distance measured from the left end of the pole, in no particular order. All input integers are not bigger than 1000000 and they are separated by whitespace.
Output

For each case of input, output two numbers separated by a single space. The first number is the earliest possible time when all ants fall off the pole (if the directions of their walks are chosen appropriately) and the second number is the latest possible such time.

样例
Sample Input

Sample Output

算法1

两只蚂蚁碰头后就各自回头 其实是一个思维陷阱， 它与两只蚂蚁碰头后就擦身而过是完全一样的
那么只要计算每次蚂蚁的最小路径选择与最大路径选择即可

#include <iostream>
#include <algorithm>

using namespace std;

/*
Sample Input

2
10 3
2 6 7
214 7
11 12 7 13 176 23 191
Sample Output

4 8
38 207

*/
#define MAX_NUM  999999

int ants[MAX_NUM];

void Do(int ants[],int len,int num)
{
    int longLen =, shortLen = ;
    for (int i = ; i < num; i++) {
        longLen = max(longLen, max(ants[i], len - ants[i]));
        shortLen = max(shortLen, min(ants[i], len - ants[i]));
    }

    cout << shortLen << " " << longLen << endl;
}

int main()
{
    int n = ;
    cin >> n;
    for (int i = ; i < n; i++) {
        int len = ; int num = ;
        cin >> len >> num;
        memset(ants,,sizeof(ants));
        for (int j = ; j < num; j++) {
            cin >> ants[j];
        }
        Do(ants,len,num);

    }
}