SPSS学习笔记参数检验—两配对样本t检验

目的：检验两个有联系的正态总体的均值是否存在显著差异。

适用条件：有联系，正态总体，样本量要一样。一般可以分为一下四种：

①同一受试对象处理前后的对比:如对于糖尿病人，对同一组病人在使用新治疗方法前测量血糖含量，在使用后再次测量血糖含量，形成两组对比样本；一般是为了说明是否有作用。

②同一受试对象不同的部位数据

③同一样品用两种方法（仪器等）检验的结果；

④配对的两个受试对象分别接受两种处理后的数据：糖尿病人按照体重进行配对（60岁的两个配对，65岁的两个配对……）然后对配对的病人采用不同的治疗方法。

案例分析：

案例描述：检验喝茶前和喝茶后体重的均值是否发生了显著的变化来确定减肥茶的减肥效果。（数据来源：《统计分析与SPSS的应用》薛薇 第五章）

题目分析：体重变化和喝茶前后有关，同时总体近似服从正态分布，因此使用两配对样本t检验。

界面操作步骤：打开数据—分析—比较均值—配对样本t检验—设置参数—输出结果

关键步骤截图：

可以有多对成对变量

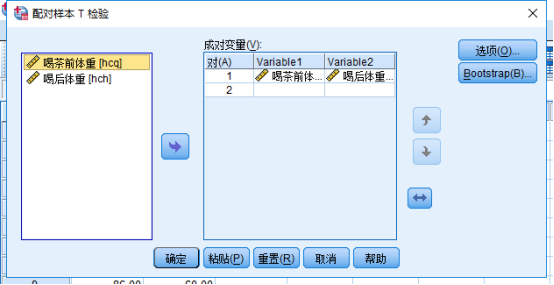
结果分析：

成对样本统计量
		均值	N	标准差	均值的标准误
对 1	喝茶前体重	89.2571	35	5.33767	.90223
	喝后体重	70.0286	35	5.66457	.95749

成对样本相关系数
		N	相关系数	Sig.
对 1	喝茶前体重 & 喝后体重	35	-.052	.768

Sig=0.768>0.05，表明服用减肥茶前后的体重并没有明显的线性变化，线性相关程度较弱。

成对样本检验
		成对差分					t	df	Sig.(双侧)
		均值	标准差	均值的标准误	差分的 95% 置信区间
					下限	上限
对 1	喝茶前体重 - 喝后体重	19.22857	7.98191	1.34919	16.48669	21.97045	14.252	34	.000

分析方法与单样本t检验类似。

注：喝茶前后相关系数越高，说明喝茶的作用其实并没有起多大作用。

参考书籍：

《统计分析与SPSS的应用》（第五版）薛薇

《SPSS统计分析从零开始》吴骏

《SPSS统计分析基础教程》张文彤