newton法分形图

方程：z^6-1=0;

%f为求解的方程，df是导数，使用的时候用funchandler定义
%res是目标分辨率，iter是循环次数，(xc,yc)是图像的中心，xoom是放大倍数
%参数视自己需求增加或减少
function newton(f,df,res,iter,xc,yc,xoom)
%一些乱糟糟的初始化
eol=1e-;
x0=xc-2.5/xoom;x1=xc+2.5/xoom;
y0=yc-2.5/xoom;y1=yc+2.5/xoom;
x=linspace(x0,x1,res);
y=linspace(y0,y1,res);
[xx,yy]=meshgrid(x,y);
z=xx+yy*1i;
kk=zeros(res,res);
tic
%对每个点进行牛顿迭代
%这个代码并行度很差，因为要对每个点单独进行一次牛顿迭代，执行速度非常慢
%明天的r参数染色我会加入并行化的算法
for m=:res
for n=:res
k=;
t=z(m,n);
ff=f(t);
while (k<=iter)&&(abs(ff)>eol)
t=t-f(t)/df(t);
ff=f(t);
k=k+;
end;
kk(m,n)=k;
end;
end;
colormap hsv;
image(x,y,kk);
axis square;
toc
end

调用：

>> f=@(z)(z^6-1);
>> df=@(z)(6*z^5);
>> newton(f,df,1024,20,0,0,1);
Elapsed time is 23.129369 seconds.

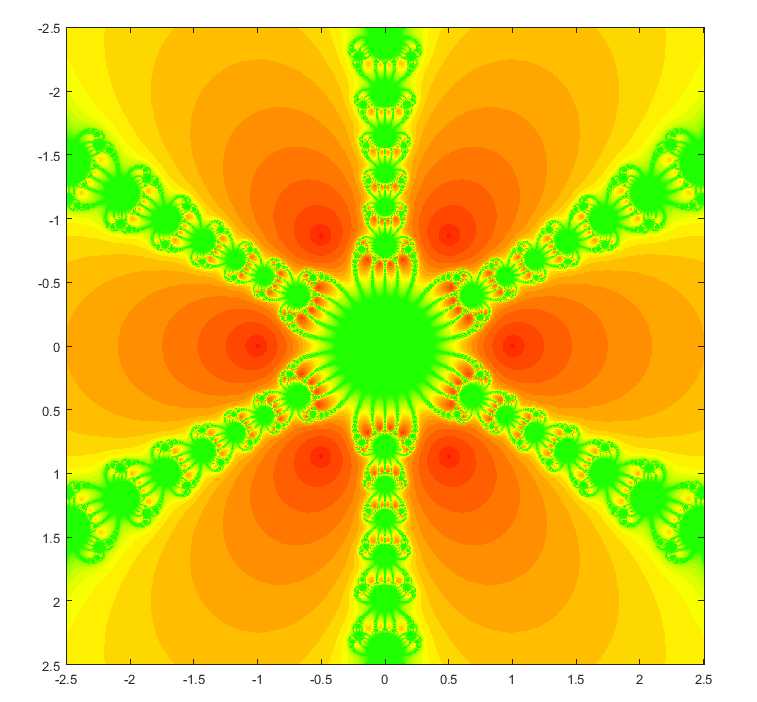
参考链接：

http://tieba.baidu.com/p/1469535720?pn=1