混沌数学之离散点集图形DEMO

最近看了很多与混沌相关的知识,并写了若干小软件.混沌现象是个有意思的东西,同时混沌也能够生成许多有意思的图形.混沌学的现代研究使人们渐渐明白，十分简单的数学方程完全可以模拟系统如瀑布一样剧烈的行为。输入端微小的差别能够迅速放大到输出端，变成压倒一切的差别,这种现象被称为“对初始条件的敏感性”。

混沌现象其基本含义可以概括为：聚散有法，周行而不殆，回复而不闭。意思是说混沌轨道的运动完全受规律支配，但相空间中轨道运动不会中止，在有限空间中永远运动着，不相交也不闭合。浑沌运动表观上是无序的，产生了类随机性，也称内在随机性。混沌系统具有三个关键要素：一是对初始条件的敏感依赖性；二是临界水平，这里是非线性事件的发生点；三是分形维，它表明有序和无序的统一。混沌系统经常是自反馈系统，出来的东西会回去经过变换再出来，循环往复，没完没了，任何初始值的微小差别都会按指数放大，因此导致系统内在地不可长期预测。

这一节将先展示下混沌点集所生成的图形.这是一个生成混沌离散点集图形的DEMO,里面含有多个不同方程生成的混沌图形.在这个DEMO中,会看到由点集生成的看得出规律的及看不出规律的图形.

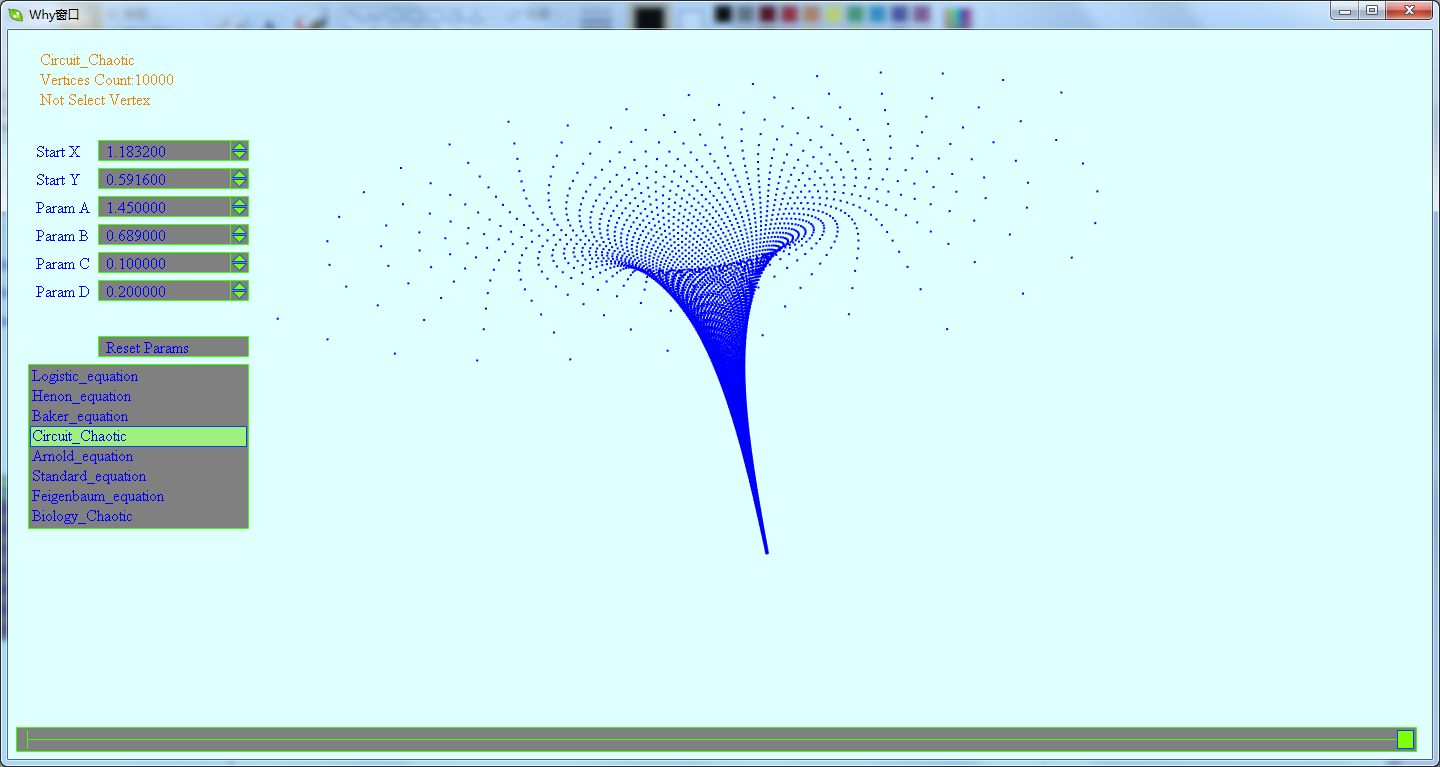
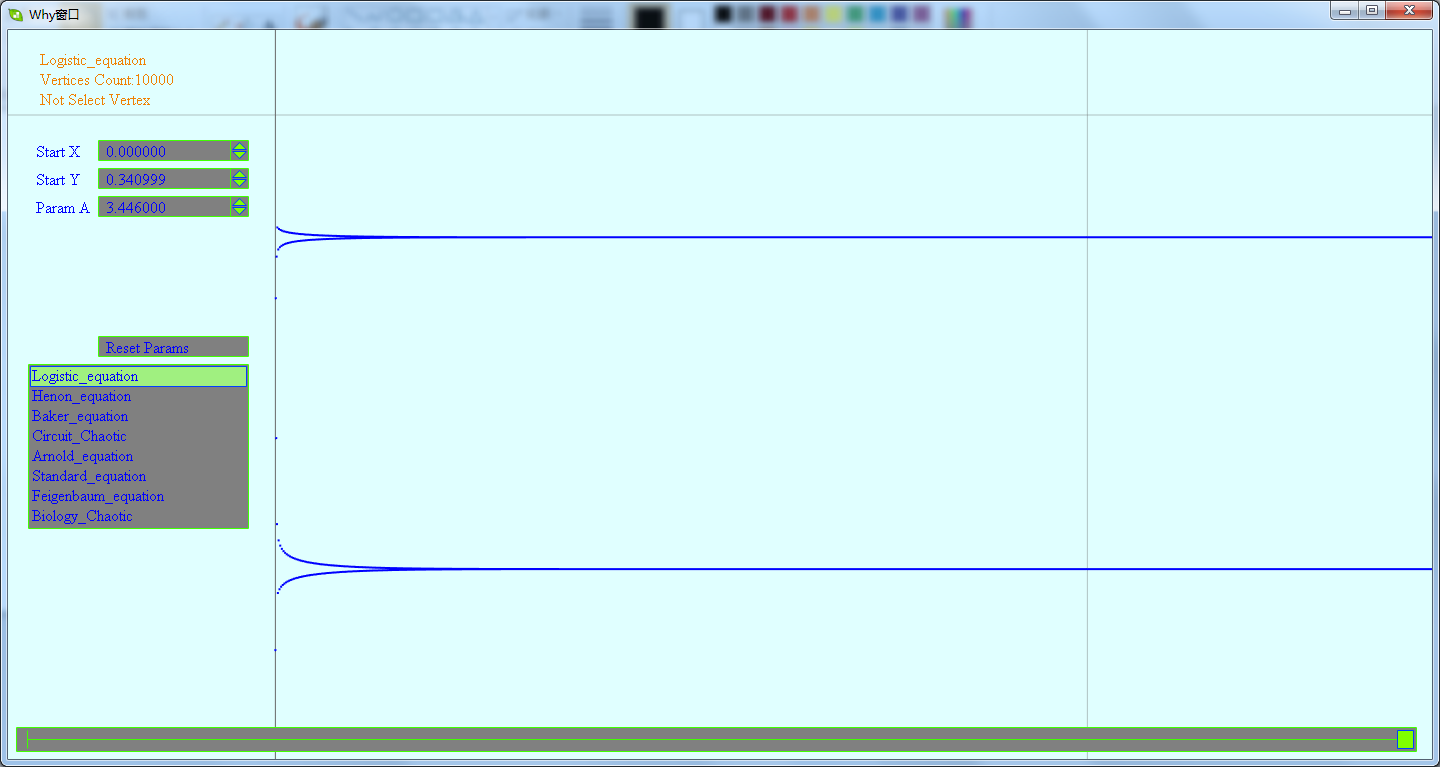
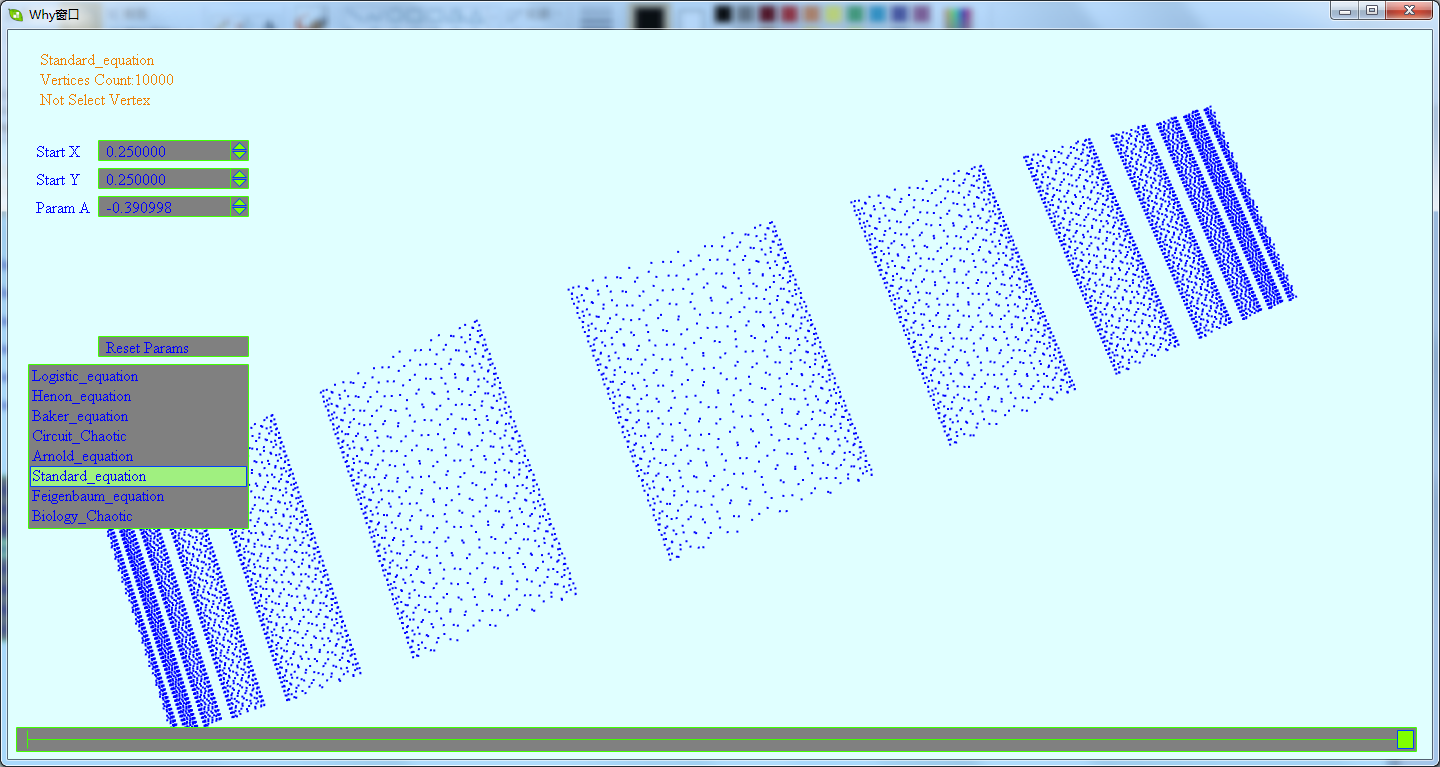
下载地址为:http://files.cnblogs.com/WhyEngine/chaos.7z

软件中有两种视口显示模式,三维和二维的.键盘O用于二者间的切换.
鼠标右键用于控制视口.

键盘G用于是否显示网格的切换

－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－

在这种离散点集的混沌图形中,使用迭代的方法生成顶点数据: 
在中学课本中我们学过，一个一元函数，通常可以表示为： Y=f(x) 这里X是自变量，Y是因变量。
例如： Y=3X+1，如果X=1，那么Y=4；如果X=4，那么Y=13；总之，如果X被确定，那么相应的Y也被确定。

我们用一个抽象的符号F，来表示Y遵循X变化的因果关系。废话连篇的解释是：数字Y随数字X的变化而变化，Y由X来决定，决定的依据是“关系”F。

如果我们利用某个关系函数，比如Y=F（X），代入一个X算出一个Y，又将Y作为新的X再次计算下一个Y………如此不断，这种方法在数学上称为迭代，具体的表达式是： Xn =F(X n-1 )，n=1,2,3……..

学过程序的人一定知道＂费波那齐数列＂，它算是比较典型的Xn =F(X n-1 )方程的例子。不过这种方程不是收敛的，所以它的图形几下就会爆表。

OK，那先帖下我写的有关这种离散方程对象的基类定义代码：

 #define SET_GET_FLOAT_PROPERTY(name) \
     void Set##name##(float v)\
     {\
         m_##name## = v;\
     }\
     float Get##name##() const\
     {\
         return m_##name##;\
     }

 #define PI 3.14159265f

 // --------------------------------------------------------------------------------------

 class DiscreteEquation
 {
 public:
     DiscreteEquation()
     {
         m_StartX = 0.0f;
         m_StartY = 0.0f;

         m_ParamA = 0.0f;
         m_ParamB = 0.0f;
         m_ParamC = 0.0f;
         m_ParamD = 0.0f;
         m_ParamE = 0.0f;
     }

     // 求迭代值
     virtual void IterateValue(float y, float z, float& outY, float& outZ) const = NULL;

     // 计算点集的Z轴坐标
     static void CalculatePointsZ(void* curveVerticesPtr, unsigned int stride, unsigned int count, float minZ, float maxZ)
     {
         char* zPtr = (char*)curveVerticesPtr + *sizeof(float);
         float zStep = (maxZ - minZ)/(count - );

         for (unsigned int i = ; i < count; i++)
         {
             *(float*)zPtr = minZ + i*zStep;
             zPtr += stride;
         }
     }

     // 计算点集的Y轴与X轴坐标
     virtual void CalculatePointsXY(void* curveVerticesPtr, unsigned int stride, unsigned int count)
     {
         char* xPtr = (char*)curveVerticesPtr;
         char* yPtr = (char*)curveVerticesPtr + sizeof(float);

         float y, x;
         float nx, ny;

         x = m_StartX;
         y = m_StartY;

         for (unsigned int i = ; i < count; i++)
         {
             *(float*)xPtr = x;
             *(float*)yPtr = y;

             IterateValue(x, y, nx, ny);

             x = nx;
             y = ny;

             xPtr += stride;
             yPtr += stride;
         }
     }

     SET_GET_FLOAT_PROPERTY(StartX);
     SET_GET_FLOAT_PROPERTY(StartY);

     SET_GET_FLOAT_PROPERTY(ParamA);
     SET_GET_FLOAT_PROPERTY(ParamB);
     SET_GET_FLOAT_PROPERTY(ParamC);
     SET_GET_FLOAT_PROPERTY(ParamD);
     SET_GET_FLOAT_PROPERTY(ParamE);

     virtual bool IsValidParamA() const {return false;}
     virtual bool IsValidParamB() const {return false;}
     virtual bool IsValidParamC() const {return false;}
     virtual bool IsValidParamD() const {return false;}
     virtual bool IsValidParamE() const {return false;}

 protected:
     float m_StartX;
     float m_StartY;

     float m_ParamA;
     float m_ParamB;
     float m_ParamC;
     float m_ParamD;
     float m_ParamE;
 };

每一种混沌点集图形，在程序中都是DiscreteEquation对象的子类．

目前，我已经实现了以下几种混沌方程，将在后来的章节中一一介绍：

（１）混沌数学之logistic模型

（２）混沌数学之二维logistic模型

（３）混沌数学之Baker模型

（４）混沌数学之CircuitChaotic(二维离散电路混沌系统)

（５）混沌数学之Arnold模型

（６）混沌数学之Standard模型

（７）混沌数学之Feigenbaum模型

（８）混沌数学之生物动力学混沌模型

（９）混沌数学之Kent模型

（１０）混沌数学之帐篷模型

（１１）混沌数学之ASin模型

（１２）混沌数学之Henon模型