【TensorFlow】一文弄懂CNN中的padding参数

在深度学习的图像识别领域中，我们经常使用卷积神经网络CNN来对图像进行特征提取，当我们使用TensorFlow搭建自己的CNN时，一般会使用TensorFlow中的卷积函数和池化函数来对图像进行卷积和池化操作，而这两种函数中都存在参数padding，该参数的设置很容易引起错误，所以在此总结下。

1.为什么要使用padding

在弄懂padding规则前得先了解拥有padding参数的函数，在TensorFlow中，主要使用tf.nn.conv2d()进行（二维数据）卷积操作，tf.nn.max_pool()、tf.nn.avg_pool来分别实现最大池化和平均池化，通过查阅官方文档我们知道其需要的参数如下：

tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None,name=None)
tf.nn.max_pool_with_argmax(input, ksize, strides, padding, Targmax=None, name=None)
tf.nn.max_pool(value, ksize, strides, padding, name=None)

这三个函数中都含有padding参数，我们在使用它们的时候需要传入所需的值，padding的值为字符串，可选值为'SAME' 和 'VALID' ；

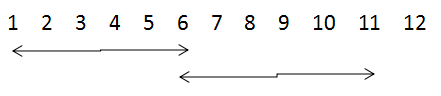
padding参数的作用是决定在进行卷积或池化操作时，是否对输入的图像矩阵边缘补0，'SAME' 为补零，'VALID' 则不补，其原因是因为在这些操作过程中过滤器可能不能将某个方向上的数据刚好处理完，如下所示：

当步长为5，卷积核尺寸为6×6时，当padding为VALID时，则可能造成数据丢失（如左图），当padding为SAME时，则对其进行补零（如右图），

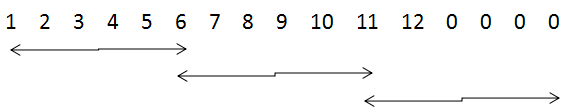
2. padding公式

首先，定义变量：

输入图片的宽和高：i_w 和 i_h

输出特征图的宽和高：o_w 和 o_h

过滤器的宽和高：f_w 和 f_h

宽和高方向的步长：s_w 和 s_h

宽和高方向总的补零个数：pad_w 和 pad_h

顶部和底部的补零个数：pad_top 和 pad_bottom

左部和右部的补零个数：pad_left 和 pad_right

1.VALID模式

输出的宽和高为

o_w = （i_w - f_w + 1）/ s_w #（结果向上取整）
o_h = （i_h - f_h + 1）/ s_h  #（结果向上取整）

2. SAME模式

输出的宽和高为

o_w = i_w / s_w#（结果向上取整）
o_h = i_h / s_h#（结果向上取整）

各个方向的补零个数为：max()为取较大值，

pad_h = max（( o_h -1 ) × s_h + f_h - i_h ， 0）
 pad_top = pad_h / 2  # 注意此处向下取整
 pad_bottom = pad_h - pad_top
 pad_w = max（( o_w -1 ) × s_w + f_w - i_w ， 0）
 pad_left = pad_w / 2 # 注意此处向下取整
 pad_right = pad_w - pad_left

3.卷积padding的实战分析

接下来我们通过在TensorFlow中使用卷积和池化函数来分析padding参数在实际中的应用，代码如下：

# -*- coding: utf-8 -*-
import tensorflow as tf

# 首先，模拟输入一个图像矩阵，大小为5*5
# 输入图像矩阵的shape为[批次大小，图像的高度，图像的宽度，图像的通道数]
input = tf.Variable(tf.constant(1.0, shape=[1, 5, 5, 1]))

# 定义卷积核，大小为2*2，输入和输出都是单通道
# 卷积核的shape为[卷积核的高度，卷积核的宽度，图像通道数，卷积核的个数]
filter1 = tf.Variable(tf.constant([-1.0, 0, 0, -1], shape=[2, 2, 1, 1]))

# 卷积操作 strides为[批次大小，高度方向的移动步长，宽度方向的移动步长，通道数]
# SAME
op1_conv_same = tf.nn.conv2d(input, filter1, strides=[1,2,2,1],padding='SAME')
# VALID
op2_conv_valid = tf.nn.conv2d(input, filter1, strides=[1,2,2,1],padding='VALID')

init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
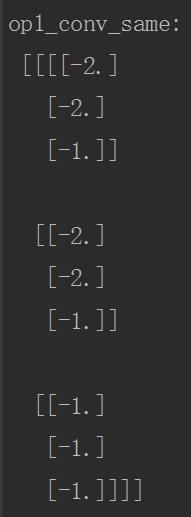
    print("op1_conv_same:\n", sess.run(op1_conv_same))
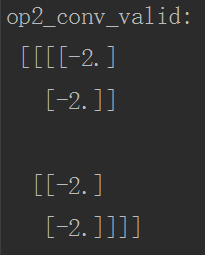
    print("op2_conv_valid:\n", sess.run(op2_conv_valid))

VALID模式的分析：

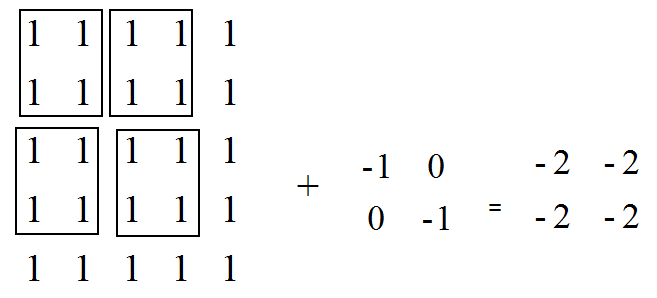
SAME模式分析：

o_w = i_w  / s_w = 5/2 = 3
o_h = i_h / s_h = 5/2 = 3

pad_w = max ( (o_w - 1 ) × s_w + f_w -  i_w , 0 )
      =  max ( (3 - 1 ) × 2 + 2 - 5 , 0 )  = 1
pad_left = 1 / 2 =0
pad_right = 1 - 0 =0
# 同理
pad_top = 0
pad_bottom = 1

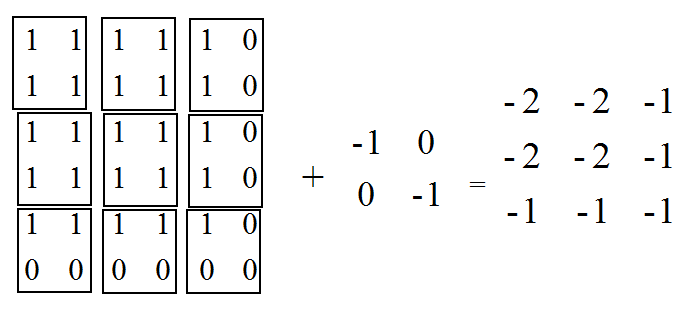
运行代码后的结果如下：

4.池化padding的实战分析

这里主要分析最大池化和平均池化两个函数，函数中padding参数设置和矩阵形状计算都与卷积一样，但需要注意的是：

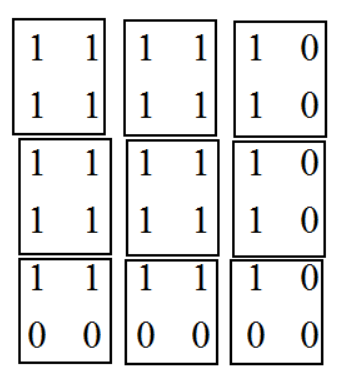
1. 当padding='SAME'，计算avg_pool时，每次的计算是除以图像被filter框出的非零元素的个数，而不是filter元素的个数，如下图，第一行第三列我们计算出的结果是除以2而非4，第三行第三列计算出的结果是除以1而非4；

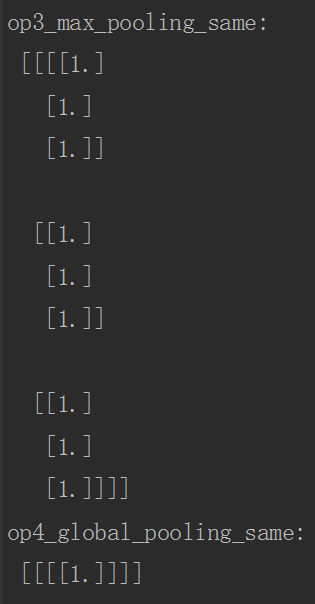
2. 当计算全局池化时，即与图像矩阵形状相同的过滤器进行一次池化，此情况下无padding，即在边缘没有补0，我们直接除以整个矩阵的元素个数，而不是除以非零元素个数（注意与第一点进行区分）

池化函数的代码示例如下：

# -*- coding: utf-8 -*-
import tensorflow as tf

# 首先，模拟输入一个特征图，大小为5*5
# 输入图像矩阵的shape为[批次大小，图像的高度，图像的宽度，图像的通道数]
input = tf.Variable(tf.constant(1.0, shape=[1, 5, 5, 1]))

# 最大池化操作 strides为[批次大小，高度方向的移动步长，宽度方向的移动步长，通道数]
# ksize为[1, 池化窗口的高，池化窗口的宽度，1]
# SAME
op1_max_pooling_same = tf.nn.max_pool(input, [1,2,2,1], strides=[1,2,2,1],padding='SAME')
# VALID
op2_max_pooling_valid = tf.nn.max_pool(input, [1,2,2,1], strides=[1,2,2,1],padding='VALID')

# 平均池化
op3_avg_pooling_same = tf.nn.avg_pool(input, [1,2,2,1], strides=[1,2,2,1],padding='SAME')
# 全局池化，filter是一个与输入矩阵一样大的过滤器
op4_global_pooling_same = tf.nn.avg_pool(input, [1,5,5,1], strides=[1,5,5,1],padding='SAME')

init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
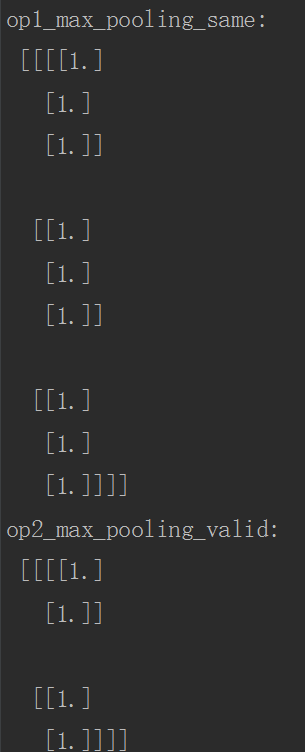
    print("op1_max_pooling_same:\n", sess.run(op1_max_pooling_same))
    print("op2_max_pooling_valid:\n", sess.run(op2_max_pooling_valid))
    print("op3_max_pooling_same:\n", sess.run(op3_avg_pooling_same))
    print("op4_global_pooling_same:\n", sess.run(op4_global_pooling_same))

运行结果如下：

 

5.总结

在搭建CNN时，我们输入的图像矩阵在网络中需要经过多层卷积和池化操作，在这个过程中，feature map的形状会不断变化，如果不清楚padding参数引起的这些变化，程序在运行过程中会发生错误，当然在实际写代码时，可以将每一层feature map的形状打印出来，了解每一层Tensor的变化。

转载请注明出处：https://www.cnblogs.com/White-xzx/p/9497029.html