pytorch求范数函数——torch.norm

torch.norm(input, p='fro', dim=None, keepdim=False, out=None, dtype=None)

返回所给tensor的矩阵范数或向量范数

参数：

• input：输入tensor
• p (int, float, inf, -inf, 'fro', 'nuc', optional)：范数计算中的幂指数值。默认为'fro'

• dim (int，2-tuple，2-list， optional): 指定计算的维度。如果是一个整数值，向量范数将被计算；如果是一个大小为2的元组，矩阵范数将被计算；如果为None，当输入tensor只有两维时矩阵计算矩阵范数；当输入只有一维时则计算向量范数。如果输入tensor超过2维，向量范数将被应用在最后一维
• keepdim（bool，optional）：指明输出tensor的维度dim是否保留。如果dim=None或out=None,则忽略该参数。默认值为False，不保留
• out（Tensor, optional）:tensor的输出。如果dim=None或out=None,则忽略该参数。
• dtype（torch.dtype，optional）：指定返回tensor的期望数据类型。如果指定了该参数，在执行该操作时输入tensor将被转换成 :attr:’dtype’

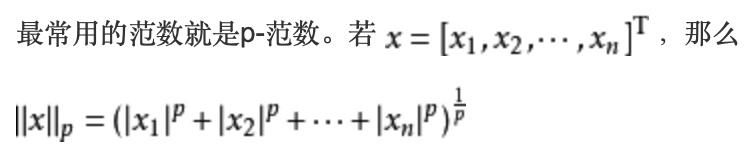
可见2范数求的就是距离

 举例说明：

>>> import torch
>>> a = torch.arange(, dtype=torch.float) -
>>> a
tensor([-., -., -., -.,  .,  .,  .,  .,  .])
>>> b = a.reshape(,)
>>> b
tensor([[-., -., -.],
        [-.,  .,  .],
        [ .,  .,  .]])
>>> torch.norm(a)
tensor(7.7460)
>>> torch.norm(b)
tensor(7.7460)

>>> torch.norm(a, float('inf'))
tensor(.)
>>> torch.norm(b, float('inf'))
tensor(.)

1）如果不指明p，则是计算Frobenius范数：

所以上面的例子中a,b的结果都相同7.7460 = √（16*2 + 9*2 +4*2 + 1*2）

2）p = 'inf',则是求出矩阵或向量中各项元素绝对值中的最大值，所以为4

>>> c = torch.tensor([[,,],[-,,]], dtype=torch.float)
>>> c
tensor([[ .,  .,  .],
        [-.,  .,  .]])
>>> torch.norm(c, dim=)
tensor([1.4142, 2.2361, 5.0000])
>>> torch.norm(c, dim=).size()
torch.Size([])
>>> torch.norm(c, dim=)
tensor([3.7417, 4.2426])
>>> torch.norm(c, p=, dim=)
tensor([., .])

1）指定dim = 0，因为c的size() = (2,3),所以会去掉其dim=0，得到size()=(3)的结果，所以是纵向求值，计算Frobenius范数

2）p=1, dim= ： 即是表示去掉维度1，使用1-范数，得到size()=(2)的结果。所以横向计算各个元素绝对值的和，为（[6,6]）

下面是多维的情况，其实结果类似：

>>> d = torch.arange(, dtype=torch.float).reshape(,,)
>>> d
tensor([[[., .],
         [., .]],

        [[., .],
         [., .]]])

>>> torch.norm(d, dim=(,))
tensor([ 3.7417, 11.2250])
>>> d.size()
torch.Size([, , ])
>>> torch.norm(d, dim=)
tensor([[4.0000, 5.0990],
        [6.3246, 7.6158]])

>>> d[,:,:]
tensor([[., .],
        [., .]])
>>> d[,:,:].size()
torch.Size([, ])

>>> torch.norm(d[,:,:])
tensor(3.7417)
>>> torch.norm(d[,:,:])
tensor(11.2250)