原文:canvas绘制贝塞尔曲线

1、绘制二次方贝塞尔曲线

quadraticCurveTo(cp1x,cp1y,x,y); 其中参数cp1x和cp1y是控制点的坐标，x和y是终点坐标

数学公式表示如下：

二次方贝兹曲线的路径由给定点P0、P1、P2的函数B（t）追踪：

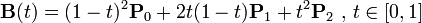
<!DOCTYPE html>

<html>

<head>

<meta charset="utf-8">

<title></title>

<style type="text/css">

*{padding: 0;margin:0;}

body{background: #1b1b1b;}

#div1{margin:50px auto; width:300px; height: 300px;}

canvas{background: #fff;}

</style>

<script type="text/javascript">

window.onload = function(){

    var c = document.getElementById('myCanvas');

    var content = c.getContext('2d');

    //绘制二次方贝塞尔曲线

    content.strokeStyle ="#FF5D43";

    content.beginPath();

    content.moveTo(0,200);

    content.quadraticCurveTo(75,50,300,200);

    content.stroke();

    content.globalCompositeOperation = 'source-over';    //目标图像上显示源图像

    //绘制上面曲线的控制点和控制线，控制点坐标为两直线的交点(75,50)

    content.strokeStyle = '#f0f';

    content.beginPath();

    content.moveTo(75,50);

    content.lineTo(0,200);

    content.moveTo(75,50);

    content.lineTo(300,200);

    content.stroke();

};

</script>

</head>

<body>

    <div id="div1">

        <canvas id="myCanvas" width="300" height="200"></canvas>

    </div>

</body>

</html>

2、三次方贝塞尔曲线

bezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y)　　其中参数cp1x，cp1y表示第一个控制点的坐标, cp2x，cp2y表示第二个控制点的坐标, x，y是终点的坐标；

数学公式表示如下：

P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1，并从P2的方向来到P3。一般不会经过P1或P2；这两个点只是在那里提供方向资讯。P0和P1之间的间距，决定了曲线在转而趋进P3之前，走向P2方向的“长度有多长”。

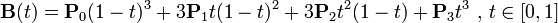
<!DOCTYPE html>

<html>

<head>

<meta charset="utf-8">

<title></title>

<style type="text/css">

*{padding: 0;margin:0;}

body{background: #1b1b1b;}

#div1{margin:50px auto; width:300px; height: 300px;}

canvas{background: #fff;}

</style>

<script type="text/javascript">

window.onload = function(){

    var c = document.getElementById('myCanvas');

    var content = c.getContext('2d');

    //三次方贝塞尔曲线

    content.strokeStyle = '#FA7E2A';

    content.beginPath();

    content.moveTo(25,175);

    content.bezierCurveTo(60,80,150,30,170,150);

    content.stroke();

    content.globalCompositeOperation = 'source-over';

    //绘制起点、控制点、终点

    content.strokeStyle = 'red';

    content.beginPath();

    content.moveTo(25,175);

    content.lineTo(60,80);

    content.lineTo(150,30);

    content.lineTo(170,150);

    content.stroke();

};

</script>

</head>

<body>

    <div id="div1">

        <canvas id="myCanvas" width="300" height="200"></canvas>

    </div>

</body>

</html>

canvas绘制贝塞尔曲线的更多相关文章

  1. 用html5的canvas画布绘制贝塞尔曲线

    查看效果:http://keleyi.com/keleyi/phtml/html5/7.htm 完整代码: <!DOCTYPE html PUBLIC "-//W3C//DTD XHT ...

  2. JavaScript+canvas 利用贝塞尔曲线绘制曲线

    效果图: <body> <canvas id="test" width="800" height="300">< ...

  3. Canvas中绘制贝塞尔曲线

    ① 什么是贝塞尔曲线? 在数学的数值分析领域中,贝济埃曲线(英语:Bézier curve,亦作“贝塞尔”)是计算机图形学中相当重要的参数曲线.更高维度的广泛化贝济埃曲线就称作贝济埃曲面,其中贝济埃三 ...

  4. HTML5 canvas绘制线条曲线

    HTML5 canvas入门 线条例子 1.简单线条 2.三角形 3.填充三角形背景颜色 4.线条颜色以及线条大小 5.二次贝塞尔曲线 6.三次贝塞尔曲线 <!doctype html> ...

  5. Unity GUI内绘制贝塞尔曲线

    用Handles可以直接在GUI下绘制贝塞尔 using UnityEditor; using UnityEngine; using System.Collections; public class ...

  6. Android 贝塞尔曲线解析

    相信很多同学都知道"贝塞尔曲线"这个词,我们在很多地方都能经常看到.利用"贝塞尔曲线"可以做出很多好看的UI效果,本篇博客就让我们一起学习"贝塞尔曲线 ...

  7. Canvas学习：封装Canvas绘制基本图形API

    Canvas学习:封装Canvas绘制基本图形API Canvas Canvas学习   从前面的文章中我们了解到,通过Canvas中的CanvasRenderingContext2D对象中的属性和方 ...

  8. canvas贝塞尔曲线

    贝塞尔曲线 Bézier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线. 曲线定义:起始点.终止点.控制点.通过调整控制点,贝塞尔曲线的形状会发生变化. 1962年,法国数学家Pierr ...

  9. [js高手之路] html5 canvas系列教程 - arcTo(弧度与二次,三次贝塞尔曲线以及在线工具)

    之前,我写了一个arc函数的用法:[js高手之路] html5 canvas系列教程 - arc绘制曲线图形(曲线,弧线,圆形). arcTo: cxt.arcTo( cx, cy, x2, y2, ...

随机推荐

  1. TabbedPaneDemo

    package swing.tabbedpane; import java.awt.BorderLayout; import java.awt.event.ActionEvent; import ja ...

  2. HDU 2454 Degree Sequence of Graph G（Havel定理 推断一个简单图的存在）

    主题链接:pid=2454">http://acm.hdu.edu.cn/showproblem.php?pid=2454 Problem Description Wang Haiya ...

  3. POJ3213(矩阵乘法)

    PM3 Time Limit: 5000MS   Memory Limit: 131072K Total Submissions: 3036   Accepted: 1059 Description ...

  4. HDOJ 4745 Two Rabbits DP

    Two Rabbits Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65535/65535 K (Java/Others) Tot ...

  5. PoolBoy

    PoolBoy  source code : https://github.com/devinus/poolboy Checkout ready({checkout, Block, Timeout}, ...

  6. js在web绘制在页上的圆

    在web页,要画一个圆.有很多方法,SVG.canvas我们能够得出. 但文章没有使用这两种方法,但使用的div.div通常一个矩形.但是,假设一个圆形的样式设置border-radius有可能div ...

  7. 编写爬虫程序的神器 - Groovy + Jsoup + Sublime（转）

    写过很多个爬虫小程序了,之前几次主要用C# + Html Agility Pack来完成工作.由于.NET FCL只提供了"底层"的HttpWebRequest和"中层& ...

  8. C++虚函数表分析

    在<<反C++>>文中提到的 VC6.0 上的编译器支持一个d1reportAllClassLayout的开关, 能够输出全部对象的内存布局信息, 我自己经常使用vs2005来 ...

  9. CSDN博客导出工具 Mac By Swift

    写这篇文章的主要目的是了解Swift语言本身,如何以及Objc和第三方交互框架 必须先用CSDN帐户登录.您可以导出所有的博客文章,加入YAML当首标信息,包括对应标签和分类在头制品信息,和底座式(原 ...

  10. Java设计模式菜鸟系列(十三)建模和实现状态模式

    转载请注明出处:http://blog.csdn.net/lhy_ycu/article/details/39829859 状态模式(State):同意对象在内部状态改变时改变它的行为,对象看起来好像 ...