leetcode 307 Range Sum Query

问题描述：给定一序列，求任意区间(i, j)的元素和；修改任意一元素，实现快速更新

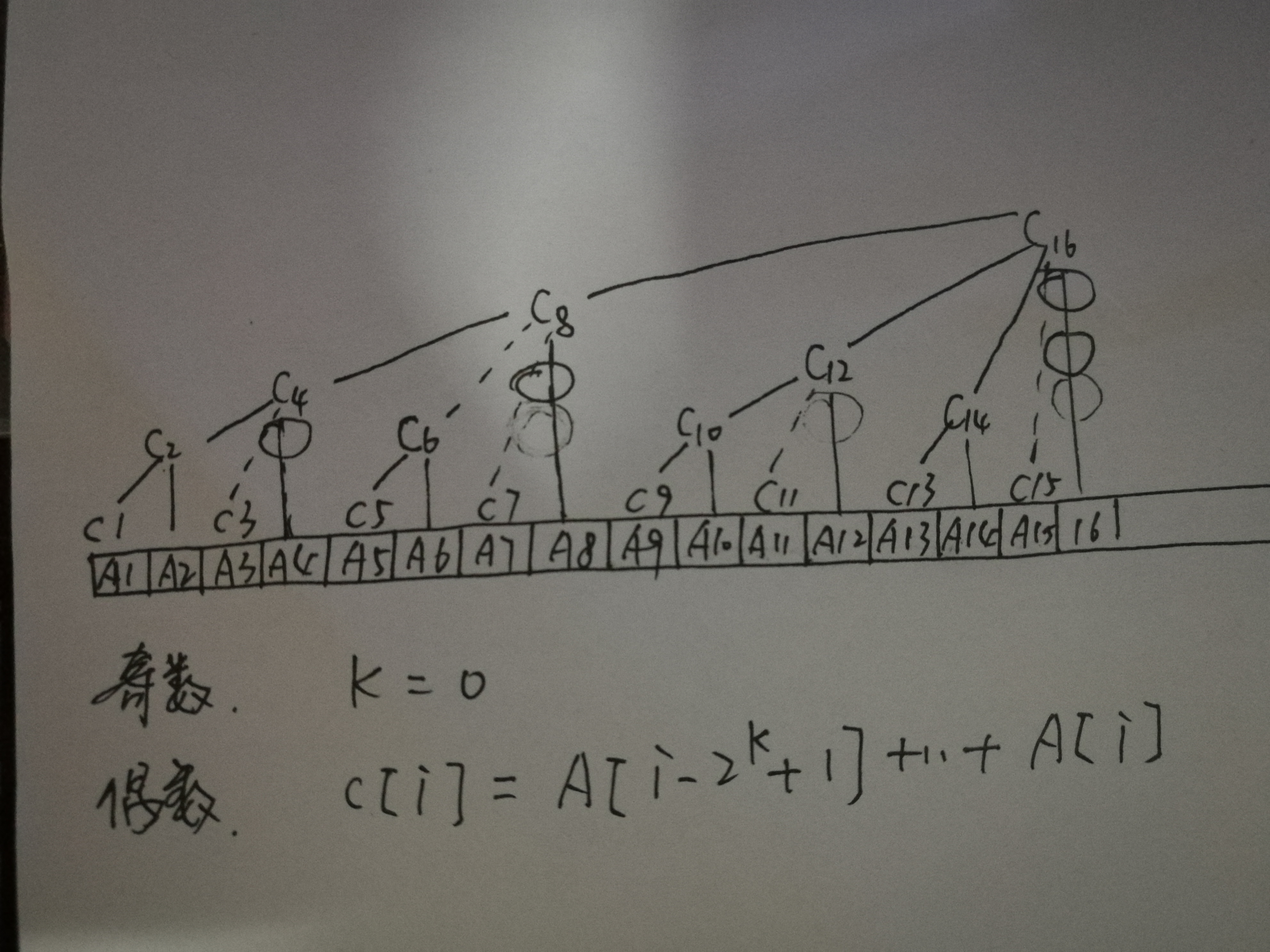
树状数组

树状数组的主要特点是生成一棵树，树的高度为logN。每一层的高度为k，分布在这一层的序列元素索引的二进制表达有个共同的特点，就是最低二次幂为k。

子树间有很强的联系，即，给定一序列元素索引i，可以推知该元素所在节点C[i]的父节点C[p]，p=i+2^k，其中k=i & (i ^ (i-1))，以及该元素所在子树的前一子树的根节点p=i-2^k。

子树间的联系可以很方便地用于求前n个元素的和，即找到所有子树即可；为实现更新，也只需要logN步操作，实现C[i]值的更新和序列元素的更新。

# leetcode 307
# 树状数组
# 树状数组的本质还是二分树，从而达到O(logN)的算法复杂度
# 树状数组最有趣的地方在于最底层高度为0，序列的第i项的高度为k，k代表i的二进制中从右数0的位数，即2次幂的最低次
# 从二进制的角度来看，很快可以得出结论 2^k = i & (i ^ (i - 1))
# 给出一节点i，可以快速找到它的父节点(i + 2^k)和该节点前的最近一棵子树的根结点(i - 2^k)
# 问题形式：
# 1. 给定一固定序列，求索引n前所有项和：相当于求所有子树的根节点值之和
# 2. 对固定序列任意修改一元素，实现快速更新：相当于更新包含该结点的所有子树的根节点的值
# 最纠结的地方还是求根节点数组C，没想到是通过update求。
class NumArray(object):
    def __init__(self, nums):
        """
        :type nums: List[int]
        """
        self.nums = [0 for _ in nums]
        self.n = len(nums)
        self.c = [0 for _ in nums]
        for i, num in enumerate(nums):
            self.update(i, num)

    def lowBit(self, x):
        ## return x & (-x)
        return x & (x ^ (x - 1))

    def update(self, i, val):
        """
        :type i: int
        :type val: int
        :rtype: void
        """
        difference = val - self.nums[i]
        self.nums[i] = val
        while i < self.n:
            self.c[i] += difference
            i += self.lowBit(i + 1)

    def getSum(self, n):
        sum = 0
        while n >= 0:
            sum += self.c[n]
            n -= self.lowBit(n + 1)
        return sum

    def sumRange(self, i, j):
        """
        :type i: int
        :type j: int
        :rtype: int
        """
        return self.getSum(j) - self.getSum(i) + self.nums[i]

        # Your NumArray object will be instantiated and called as such:
        # obj = NumArray(nums)
        # obj.update(i,val)
        # param_2 = obj.sumRange(i,j)

nums = [1, 3, 5]
X = NumArray(nums)
# X.update(0, 1)
print(X.sumRange(0, 2))
# print(X.getSum(0))

线段树

线段树是一种满二分树，即每个节点的度为0或2.

线段树的主要特点是不断平分区间[s, e]为[s, mid]和[mid + 1, e]，其中mid = s + int((e - s) / 2)。称度为0的结点为叶节点，即只包含一个数，不再平分。

线段树的构造是通过构造结点，由其平分性质可知，若给定序列长度为N，则叶节点数目为N，非叶节点为N - 1，即一共2N - 1个结点。

定义根节点的索引为0，其左子树的结点为1， 右子树的结点为2。通用地说，若当前结点为i，则其左结点为(2 * i + 1)，右结点为(2 * i + 2)，因此，构造结点数目时，索引长度不是N-1。（具体为多少我也还不知道，有博文说是2 * 2 ^(ceil(logN))） - 1，但数据量一大leetcode上就死活通不过）

同样地，线段树可以用于求和和更新。非常巧妙！线段树的操作基本都是基于递归函数，先给一个总区间（也就是根节点对应的区间），然后不断平分，求 getSbSumUntil(ss, mid, qs, qe, (2 * si) + 1) +
getSbSumUntil(mid + 1, se, qs, qe, (2 * si) + 2)

此外，线段树还可以用于求区间和最大和区间替换，下次说。

# leetcode 307
# 线段树
import math
class NumArray(object):
    def __init__(self, nums):
        """
        :type nums: List[int]
        """
        self.nums = nums
        self.n = len(nums)
        self.st = [0 for _ in range(2 * 2 ^ int(math.log2(self.n)))]
        self.constructSTUntil(0, self.n - 1, 0)

    def getMid(self, s, e):
        return int(s + (e - s) / 2)

    def constructSTUntil(self, ss, se, si):
        if ss == se:
            self.st[si] = self.nums[ss]
            return self.st[si]
        mid = self.getMid(ss, se)
        self.st[si] = self.constructSTUntil(ss, mid, (2 * si) + 1) + \
                      self.constructSTUntil(mid + 1, se, (2 * si) + 2)
        return self.st[si]

    def updataUntil(self, ss, se, i, si, difference):
        if i < ss or i > se:
            return
        self.st[si] += difference
        if ss != se:
            mid = self.getMid(ss, se)
            self.updataUntil(ss, mid, i, (2 * si + 1), difference)
            self.updataUntil(mid + 1, se, i, (2 * si + 2), difference)

    def update(self, i, val):
        """
        :type i: int
        :type val: int
        :rtype: void
        """
        difference = val - self.nums[i]
        self.nums[i] = val
        self.updataUntil(0, self.n - 1, i, 0, difference)

    def getSbSumUntil(self, ss, se, qs, qe, si):
        if qs == qe:
            return self.nums[qs]
        if (qs <= ss) and (qe >= se):
            return self.st[si]
        if (qs > se) or (qe < ss):
            return 0
        mid = self.getMid(ss, se)
        return self.getSbSumUntil(ss, mid, qs, qe, (2 * si) + 1) + \
               self.getSbSumUntil(mid + 1, se, qs, qe, (2 * si) + 2)

    def sumRange(self, i, j):
        """
        :type i: int
        :type j: int
        :rtype: int
        """
        return self.getSbSumUntil(0, self.n - 1, i, j, 0)

        # Your NumArray object will be instantiated and called as such:
        # obj = NumArray(nums)
        # obj.update(i,val)
        # param_2 = obj.sumRange(i,j)

nums = [-1]
X = NumArray(nums)
X.update(0, 1)
print(X.sumRange(0, 0))

　参考文献：

http://bookshadow.com/weblog/search/?pattern=%E7%BA%BF%E6%AE%B5%E6%A0%91&submit=

http://www.cnblogs.com/newpanderking/articles/2775168.html