POJ 3070(求斐波那契数 矩阵快速幂)

题意就是求第 n 个斐波那契数。

由于时间和内存限制，显然不能直接暴力解或者打表，想到用矩阵快速幂的做法。

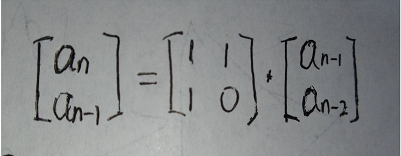
代码如下：

 #include <cstdio>
 using namespace std;
 const int maxn = ;
 const int mod = ;
 int a;
 struct Matrix
 {
     int m[maxn][maxn];
 }ans,res,w,head;

 Matrix mul(Matrix a,Matrix b,int n)
 {
     Matrix tmp;
     for(int i = ; i <= n; i++)
         for(int j = ; j <= n; j++)
             tmp.m[i][j] = ;
     for(int i = ; i <= n; i++)
         for(int j = ; j <= n; j++)
             for(int k = ; k <= n; k++)
                 tmp.m[i][j] += ((a.m[i][k] % mod)*(b.m[k][j] % mod))%mod;
     return tmp;
 }

 void quickpow(int N,int n)
 {
     for(int i = ; i <= n; i++)
         for(int j = ; j <= n; j++)
             if(i == j)  ans.m[i][j] = ;
             else ans.m[i][j] = ;
     while(N)
     {
         if(N&) ans = mul(ans,res,);
         res = mul(res,res,);
         N = N >>;
     }
 }

 int main()
 {
     while(scanf("%d",&a))
     {
         if(a == -) break;
         else if(a == )
         {
             puts("");
             continue;
         }
         head.m[][] = head.m[][] = head.m[][] = ;
         head.m[][] = ;
         res.m[][] = res.m[][] = res.m[][] = ;
         res.m[][] = ;
         quickpow(a,);
         w = mul(ans,head,);
         printf("%d\n",w.m[][]);
     }
     return ;
 }