洛谷P2327 [SCOI2005] 扫雷

题目描述

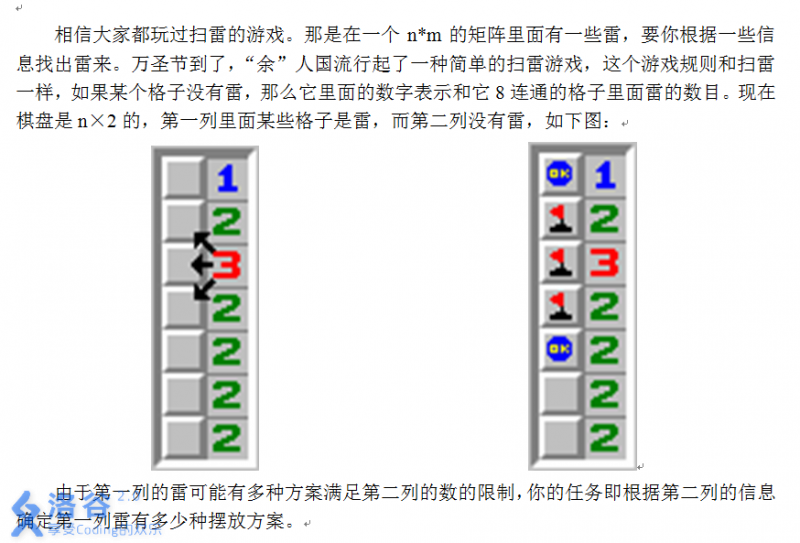
输入输出格式

输入格式：

第一行为N，第二行有N个数，依次为第二列的格子中的数。（1<= N <= 10000）

输出格式：

一个数，即第一列中雷的摆放方案数。

输入输出样例

输入样例#1：

2
1  1

输出样例#1：

2

迷之DP，如果没看算法标签，可能会想岔到数学方向。

一个数字会影响它正左、左上、左下三个格子的方案。考虑左边和左上两个方向的地雷数，可以推出左下是否有雷。

然而这样考虑，决策似乎是有后效性的。改为枚举左上情况，考虑左边和左下两个方向的雷数。

方程写了一长串……

 /*by SilverN*/
 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<vector>
 using namespace std;
 const int mxn=;
 int read(){
     int x=,f=;char ch=getchar();
     while(ch<'' || ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>='' && ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 int n;
 int f[mxn][];
 int w[mxn];
 //f[][0] 左边和左下没有雷
 //f[][1] 仅左下有雷
 //f[][2] 仅左边有雷
 //f[][3] 左边和左下有雷
 int main(){
     n=read();
     for(int i=;i<=n;i++) w[i]=read();
     if(w[]==){f[][]=;}
     else if(w[]==){f[][]=f[][]=;}
         else if(w[]==){f[][]=;}
     for(int i=;i<n;i++){
         if(w[i]==)
             f[i][]=f[i-][];
         if(w[i]==){
             f[i][]+=f[i-][];
             f[i][]+=f[i-][];
             f[i][]+=f[i-][];
         }
         if(w[i]==){
             f[i][]+=f[i-][];
             f[i][]+=f[i-][];
             f[i][]+=f[i-][];
         }
         if(w[i]==){
             f[i][]=f[i-][];
         }
     }
     if(w[n]==)printf("%d\n",f[n-][]+f[n-][]);
     if(w[n]==)printf("%d\n",f[n-][]);
     if(w[n]==)printf("0\n");
     if(w[n]==)printf("%d\n",f[n-][]);
     return ;
 }