FFT 快速傅里叶变换浅析

终于补完坑了哈哈哈

这个东西很神奇，看了半天网上的解释和课件，研究了很长时间，算是大概明白了它的原理。

话不多说先上图。

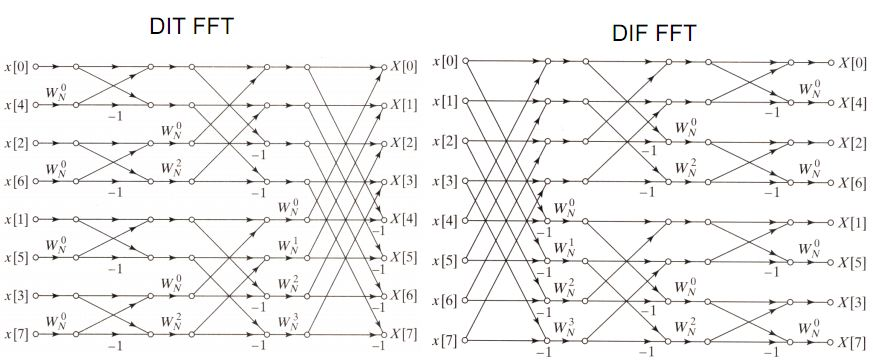
我们要求的h(x)=f(x)*g(x),f(x)=Σai*x^i,g(x)=Σbi*x^i.

朴素求复杂度是$n^2$的，但一个$x$次多项式在平面上可以由$x+1$个点唯一插值表示，所以我们可以先用求出$x+1$个点$(xi,f(xi))$和$(xi,g(xi))$，再求出$(xi,f(xi)*g(xi))$，就可以反解出$h(x)$的表达式。

那么我们需要在$nlogn$的时间内干完这两步，首先xi的取值需要特殊取，令$xi=ζ_{n}^i$（不懂复数的同学可以自行百度），令n(多项式次数，不够的话也要补)=$2^m$，那么

$(ζ_n^k=ζ_{n/2}^{k/2})$

这显然是一个分治的形式，一个节点可以转移到下一层的两个节点，而每个节点又由上一层的两个节点转移，一共$logn$层，所以复杂度是$nlogn$的。

所以按这个式子分治下去，a0,a2,a4会不停排到前边去，最后的顺序变成图里的0,4,2,6,1,5,3,7，即把它们的二进制补零后翻转然后重新排序（证明很好证，可以自行脑补）。

放代码。

    typedef complex<double> E;
    for (int i = ; i < n; i <<= )
    {
        E wn(cos(pi / i), f*sin(pi / i));
        for (int j = ; j < n; j += (i << ))
        {
            E w(, );
            for (int k = ; k < i; k++, w *= wn)
            {
                E x = a[j + k],y=w*a[j+k+i];
                a[j + k] = x + y; a[j + k + i] = x - y;
            }
        }
    }

第一个循环枚举每回合并的区间长度，然后j每回跳2*i个单位，前i个由x+y转移，后i个由x-y转移，对应图上由左边和左下转移的点和由左边和左上转移的点，至于为什么这么转移。。。。。

第i层第k(从0开始)个节点代表的意义是把ζ(2^i,k%(2^i))带进一个多项式里所得的值,多项式为a0+a1*x+a2*x^2......,其中a数组是排好序的，举个例子：第二列第一个点是

a0+a4(原数组的第四个)*x,第三个点为a2+a6*x,第四个也为a2+a6*x(不过因为x不同所以值不同),第三列第五个为a1+a5*x+a3*x^2+a7*x^3。

又因为ζ(n,k)=-ζ(n,k+n/2)，参考分治形式转移就很好解释了。

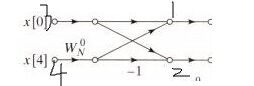
1号点的x=ζ(2,0)，二号点为ζ(2,1)，

f1=a0+a4*ζ(2,0)=f(3)+f(4)*ζ(2,0),

f2=a0+a4*ζ(2,1)=a0-a4*ζ(2,2)=a0-a4*ζ(2,0)=f(3)-f(4)*ζ(2,0)。

这就可以解释代码中w值相同但一个正一个负了。

（有什么不懂的地方可以留言，我会及时补充的>_<）。

（感谢lty大佬的帮助 ）。