队列（FIFO）—循环队列、队列的链式存储

1 队列的定义

队列是只允许在一端（队尾）进行插入操作，而在另一端（队头）进行删除操作的线性表。

2 队列的特点

1）先进先出是队列最大的特点，是应用中非常常见的模型，例如排队；

2）队列也属于线性表，线性表的特性队列都拥有。

3 循环队列的实现及关键点

3.1 关键点

1）队列为空的条件：队头指针等于队尾指针，即head == tial；

2）队列中保留一个元素空间，当队列满时，尾指针和头指针之间还剩一个元素空间。队列为满的条件：(tial + 1) % quenceSize == head；

3）队列中元素个数为：(tial + quenceSize - head) % quenceSize。

3.2 实现

 #ifndef CYCLESQUENCE_H
 #define CYCLESQUENCE_H

 typedef int ElemType;

 class CycleQuence {
 private:
     ElemType* m_pData;    //数组地址
     int m_nHead;    //首元素位置
     int m_nTial;    //尾元素位置
     int m_nMaxSize;    //数组长度

 public:
     CycleQuence(int maxSize);
     ~CycleQuence();
     void ClearQuence() { m_nHead = , m_nTial = ; }    //清空队列
     bool EnterQuence(ElemType elem);    //入队
     bool DeleteQuence(ElemType* pElem);    //出队
     void VisitQuence() const;    //查看队列元素
     bool IsEmpty() const { return m_nHead == m_nTial; }    //判断是否为空
     bool IsFull() const { return m_nHead == (m_nTial + ) % m_nMaxSize; }    //判断是否为满
 };

 #endif

 #include "pch.h"
 #include "CycleSquence.h"
 #include <iostream>

 CycleQuence::CycleQuence(int maxSize)
 {
     m_nHead = ;
     m_nTial = ;
     m_nMaxSize = maxSize;
     m_pData = new ElemType[maxSize];
 }

 CycleQuence::~CycleQuence()
 {
     delete[] m_pData;
 }

 bool CycleQuence::EnterQuence(ElemType elem)    //入队
 {
     if (IsFull())    //队满
     {
         std::cout << "The quence is full." << std::endl;
         return false;
     }

     m_pData[m_nTial] = elem;
     m_nTial = (m_nTial + ) % m_nMaxSize;
     VisitQuence();

     return true;
 }

 bool CycleQuence::DeleteQuence(ElemType* pElem)    //出队
 {
     if (IsEmpty())    //队空
         return false;

     *pElem = m_pData[m_nHead];
     m_nHead = (m_nHead + ) % m_nMaxSize;
     VisitQuence();

     return true;
 }

 void CycleQuence::VisitQuence() const    //查看队列元素
 {
     std::cout << "The element of quence: ";
     for (int i = m_nHead, j = ; j < (m_nTial + m_nMaxSize - m_nHead) % m_nMaxSize; i = (i + ) % m_nMaxSize, ++j)
         std::cout << m_pData[i] << ' ';
     std::cout << std::endl;
 }

测试代码（Visual Studio 2017上测试）：

 #include "pch.h"
 #include "CycleSquence.h"
 #include <iostream>

 int main()
 {
     CycleQuence quence();
     quence.EnterQuence();
     quence.EnterQuence();
     quence.EnterQuence();
     quence.EnterQuence();
     ElemType elem;
     quence.DeleteQuence(&elem);
     quence.DeleteQuence(&elem);
     quence.DeleteQuence(&elem);
     quence.EnterQuence();
     quence.EnterQuence();
     quence.EnterQuence();
     quence.EnterQuence();

     return ;
 }

测试结果：

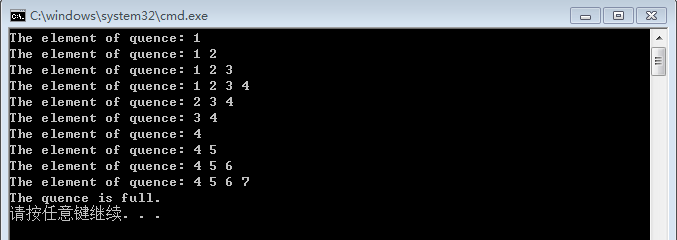
在写VisitQuence()这个方法时，想了好一会儿，就是想可不可以用一个变量遍历队列。但是其实没必要这样，代码在执行效率差不多的情况下，更要注重清晰易懂，简洁的代码有时更容易让人费解。

4 队列的链式存储的实现和关键点

4.1 关键点

1）链队列为空的条件为：head == tial;

2）队列的链式存储通过单链表实现，尤其注意入队、出队操作。

4.2 实现

略。

该篇博客是自己的学习博客，水平有限，如果有哪里理解不对的地方，希望大家可以指正！