题解：[NOIP2016 提高组] 蚯蚓

洛谷同步链接

题目传送门

前置结论

结论

对于整数 $x_1,x_2$ ，当 $x_1\geq x_2,0<p<1$ 时有：

1. $\lfloor px_1 \rfloor \geq \lfloor px_2 \rfloor$
2. $x_1 -\lfloor px_1 \rfloor \geq x_2- \lfloor px_1 \rfloor$

证明

结论 $1$ 显然得证。

结论 $2$ 证明参见此处。以下为转载内容。

2024 年 7 月更新：新版蓝书受我反馈，已经更正此问题。

本题中所有题解的单调性正确性似乎都有或多或少的问题，在这里我给出一个严谨的单调性证明。

首先：$x - \lfloor px \rfloor$ 这个函数并不是单调不降的，它只在整点上单调不降，可以在 desmos 中画一个 $x - \lfloor 0.9x \rfloor$ 的函数试试看，你会发现它并没有单调性。当然，$x - px$ 有单调性。

所以一切直接抛开下取整对单调性的证明是没有任何道理的，这就叉掉了本题大量题解，包括但不限于第一篇题解。

同时，一切没有用到 $x_1$，$x_2$ 这两个数为整数这个性质就证出了这个函数的单调性的都是伪证，本题疑似所有题解全都是伪证。lyd 蓝书上的证明也是伪证，具体原因见下。

前置知识：

• 下取整函数单调不降，即对于 $x_1 < x_2$ 有 $\lfloor x_1\rfloor \le \lfloor x_2 \rfloor$；
• 整数可以自由移入移出下取整函数，即对于 $z \in \mathbb Z$，有 $\lfloor x \rfloor + z = \lfloor x + z \rfloor$。
• 注意：负号不能随便移入移出，$\lfloor -3.4 \rfloor \ne - \lfloor 3.4 \rfloor$。
• 关于这点很容易犯的一个错误就是对于 $z \in \mathbb Z$，有$\lfloor z - x \rfloor = z - \lfloor x \rfloor$，事实上这点根本不成立，举个反例：$\lfloor 1 - 0.3 \rfloor \ne 1 - \lfloor 0.3\rfloor$。
• 刚刚这条错误就是很多伪证的错误原因所在，包括 lyd 蓝书的证明也存在这个伪证。

真正证明：

命题：对于 $x_1, x_2 \in \mathbb Z, x_1 \ge x_2, 0< p < 1$，有 $x_1 - \lfloor px_1 \rfloor \ge x_2 - \lfloor px_2 \rfloor$。

证明：$x_1 \ge x_2 \land x_1, x_2 \in \mathbb Z$，因此 $x_1 - x_2 \in \mathbb N$。又因为 $0 <p < 1$，所以：

$$

\begin{aligned}

x_1 - x_2 &\ge p(x_1 - x_2)\

x_1 - x_2 + p x_2 & \ge px_1 \

\lfloor px_2 + (x_1 - x_2) \rfloor & \ge\lfloor px_1 \rfloor \

\lfloor px_2 \rfloor + (x_1 - x_2) & \ge \lfloor px_1 \rfloor \

x_1 - \lfloor px_1 \rfloor & \ge x_2 - \lfloor px_2 \rfloor

\end{aligned}

$$

证明出了这一点的单调性之后，事实上我们就解决了 $q = 0$ 的单调性问题，接下来解决 $q \ge 0$ 的。

我们假设某一秒，我们切开了一个数 $x_1$，下一秒，我们切开了一个数 $x_2 + q$。$x_2 + q$ 在上一秒时为 $x_2$，因此 $x_1 \ge x_2$。我们的证明目标是 $\lfloor px_1\rfloor+ q \ge \lfloor p(x_2 + q)\rfloor$ 和 $x_1 - \lfloor px_1\rfloor+ q \ge x_2 + q - \lfloor p(x_2 + q)\rfloor$。

需要注意这个证明目标也有很多题解搞错，lyd 蓝书此处的证明存在上面所说的问题（那条假结论）。

对于第一条：$\lfloor px_1\rfloor+ q = \lfloor px_1 + q\rfloor \ge \lfloor px_2 + pq\rfloor = \lfloor p(x_2 + q)\rfloor$。

对于第二条：$x_1 - \lfloor px_1\rfloor+ q \ge x_2 +q - \lfloor px_2\rfloor \ge x_2 + q - \lfloor p(x_2 +q) \rfloor$。这里第一个不等号用了 $q = 0$ 的证明结论。

---

不知道你们有没有这个疑问，我补一下。https://www.luogu.com.cn/discuss/551666

其中，$\color{blue}{x -\lfloor px\rfloor}\color{black}{,}\ \color{red}{x-px}$ 图像如此：

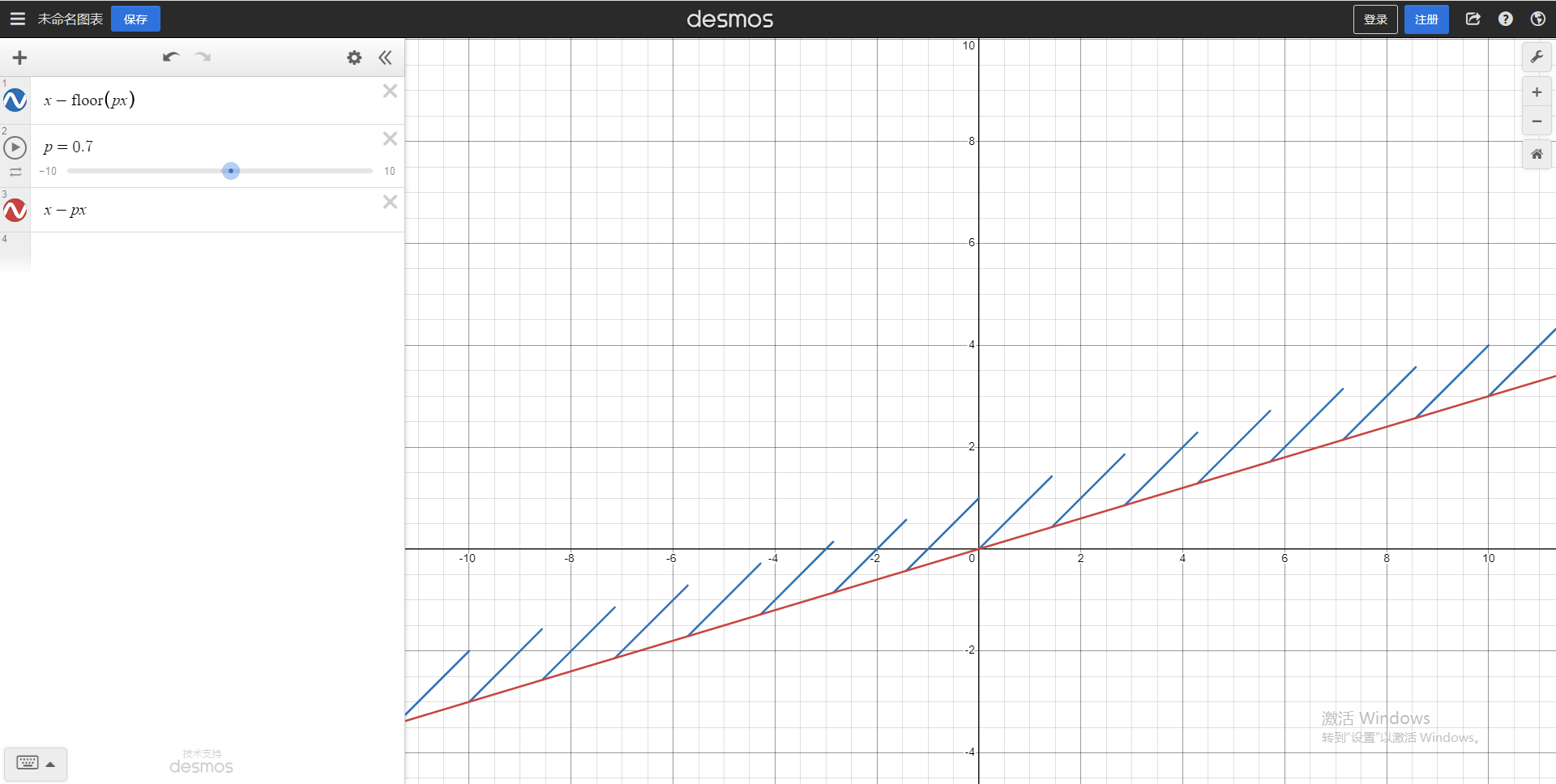
处理切割

数据结构

维护三个队列 $Q_1,Q_2,Q_3$：

• $Q_1$ 为未曾切割的蚯蚓；
• $Q_2$ 为切割时形如 $\lfloor px \rfloor$ 的蚯蚓；
• $Q_3$ 为切割时形如 $x- \lfloor px \rfloor$ 的蚯蚓。

操作

模拟题意：每次取最长蚯蚓进行切割。

首先维持 $Q_1$ 单调不增，然后根据前置结论 $2$ ，取最长蚯蚓进行切割所得的两条蚯蚓也比其他蚯蚓切割所得蚯蚓长。

举个例子：

蚯蚓长为 $10,8,7$，$p=0.3$。则切割所得蚯蚓长为 $(3,7),(2,6),(2,5)$，括号表示由同一蚯蚓切割所得。

这样，我们每次在 $Q_1,Q_2,Q_3$ 里查询最大值，切割后加入 $Q_2,Q_3$ 就可以维持 $Q_2,Q_3$ 单调。那么我们只需要取队首比较即可。

输出

第一行

输出也只需要 $i \in [1,m]$ 模拟每一秒，$i \bmod t=0$ 时输出队首即可。

第二行

从大到小查找队首输出并出队即可。

---

考虑到蚯蚓每一秒都会增长 $q$，我们考虑是否可能 $\mathcal O(1)$ 处理。

不妨令 $i$ 秒时，$q=pl$。

那么我们记录蚯蚓加入队列时的已增加长度 $pl'$，最后用原有长度加上 $pl-pl'$ 即可。

那么我们只需要在加入队列时，加入 $\lfloor px \rfloor-pl'$ 即可。

由于所有蚯蚓都减去了 $pl'$，并不影响 $Q_1,Q_2,Q_3$ 的单调性。

AC代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int M=7e6;
int n,m,q,u,v,t;
//Q:手写队列(节约空间)
int Q[4][M+1],front[4],rear[4];
bool cmp(int a,int b){
	return a>b;
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/

	scanf("%d %d %d %d %d %d",&n,&m,&q,&u,&v,&t);
	for(int i=1;i<=n;i++)scanf("%d",&Q[1][i]);
	front[1]=front[2]=front[3]=1;
	rear[1]=n;
	sort(Q[1]+1,Q[1]+n+1,cmp);//单调不增
	int pl=0;
	//第一行
	for(int i=1;i<=m;i++){
		//查找队首最大值
		int o,Max=-2147483648;
		for(int j=1;j<=3;j++){
			if(front[j]<=rear[j]&&Q[j][front[j]]>Max){
				Max=Q[j][front[j]];
				o=j;
			}
		}front[o]++;//出队
		Max+=pl;pl+=q;
		int x=1ll*Max*u/v;
		//切割并入队
		Q[2][++rear[2]]=x-pl;
		Q[3][++rear[3]]=Max-x-pl;
		if(i%t==0)printf("%d ",Max);//输出
	}putchar(10);//换行
	//第二行
	for(int i=1;i<=m+n;i++){
		//从大到小查找、输出即可。
		//同理
		int o,Max=-2147483648;
		for(int j=1;j<=3;j++){
			if(front[j]<=rear[j]&&Q[j][front[j]]>Max){
				Max=Q[j][front[j]];
				o=j;
			}
		}front[o]++;
		if(i%t==0)printf("%d ",Max+pl);
	}

	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}