day39 算法基础

参考博客：

• http://www.cnblogs.com/alex3714/articles/5474411.html
• http://www.cnblogs.com/wupeiqi/articles/5480868.html

第一部分 算法简单概念

• 算法概念
• 复习：递归
• 时间复杂度
• 空间复杂度

什么是算法？

• 算法（Algorithm）：一个计算过程，解决问题的方法

复习：递归

• 递归的两个特点：
  • 调用自身
  • 结束条件
• 看下面几个函数：

递归：练习

时间复杂度

• 看代码：

• • print('Hello World')

• • for i in range(n):
  • 　　print('Hello World')

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

• • for i in range(n):
  • 　　for j in range(n):
  • 　　　　print('Hello World')

• • for i in range(n):
  • 　　for j in range(n):
  • 　　　　for k in range(n):
  • 　　　　　　print('Hello World')

 上面四组代码，哪组运行时间最短？
 用什么方式来体现代码（算法）运行的快慢？

• 类比生活中的一些事件，估计时间：
  • 眨一下眼　　                      一瞬间/几毫秒
  • 口算“29+68”                        几秒
  • 烧一壶水                              几分钟
  • 睡一觉                                 几小时
  • 完成一个项目                      几天/几星期/几个月
  • 飞船从地球飞出太阳系        几年
• 时间复杂度：用来评估算法运行效率的一个东西

　　

• 那这些代码呢？

　　

• 那这个代码呢？

　　

• 时间复杂度-小结
  • 时间复杂度是用来估计算法运行时间的一个式子（单位）。
  • 一般来说，时间复杂度高的算法比复杂度低的算法慢。
  • 常见的时间复杂度（按效率排序）
    • O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n3)
  • 不常见的时间复杂度（看看就好）
    • O(n!) O(2n) O(nn) …
  • 如何一眼判断时间复杂度？
    • 循环减半的过程O(logn)
    • 几次循环就是n的几次方的复杂度

空间复杂度

• 空间复杂度：用来评估算法内存占用大小的一个式子
• “空间换时间”

列表查找

• 列表查找：从列表中查找指定元素
  • 输入：列表、待查找元素
  • 输出：元素下标或未查找到元素
• 顺序查找
  • 从列表第一个元素开始，顺序进行搜索，直到找到为止。
• 二分查找
  • 从有序列表的候选区data[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。

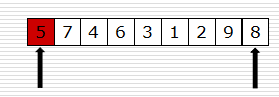
二分查找

• 使用二分查找来查找3

　　

列表查找-代码

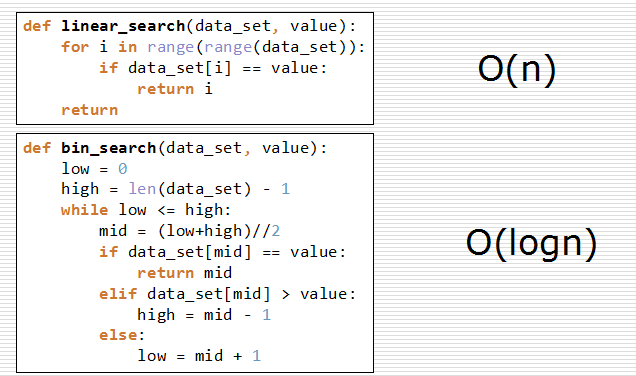
递归版本的二分查找

def bin_search_rec(data_set, value, low, high):
    if low <= high:
        mid = (low + high) // 2
        if data_set[mid] == value:
            return mid
        elif data_set[mid] > value:
            return bin_search_rec(data_set, value, low, mid - 1)
        else:
            return bin_search_rec(data_set, value, mid + 1, high)
    else:
        return

列表查找：练习

• 现有一个学员信息列表（按id增序排列），格式为：

[
{id:1001, name:"张三", age:20},
{id:1002, name:"李四", age:25},
{id:1004, name:"王五", age:23},
{id:1007, name:"赵六", age:33}
]

• 修改二分查找代码，输入学生id，输出该学生在列表中的下标，并输出完整学生信息。

• Letcode

• 34. Search for a Range (二分查找升级版)

• 1. Two Sum

列表排序

• 列表排序
  • 将无序列表变为有序列表
• 应用场景：
  • 各种榜单
  • 各种表格
  • 给二分排序用
  • 给其他算法用
• 输入：无序列表
• 输出：有序列表
• 升序与降序
• 排序low B三人组：
  • 冒泡排序
  • 选择排序
  • 插入排序
• 快速排序
• 排序NB二人组：
  • 堆排序
  • 归并排序
• 没什么人用的排序：
  • 基数排序
  • 希尔排序
  • 桶排序

排序Low B三人组

• 大家自己能想到怎么完成一次排序吗？
• 冒泡排序
• 选择排序
• 插入排序
• 算法关键点：
  • 有序区
  • 无序区

冒泡排序思路

• 首先，列表每两个相邻的数，如果前边的比后边的大，那么交换这两个数……
• 会发生什么？

　　

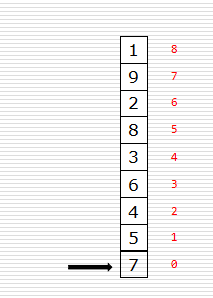
• 代码关键点：
  • 趟
  • 无序区

• 冒泡排序代码

def bubble_sort(li):
    for i in range(len(li)-1):
        for j in range(len(li)-i-1):
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]

• 时间复杂度：O(n2)
• 冒泡排序-优化
  • 如果冒泡排序中执行一趟而没有交换，则列表已经是有序状态，可以直接结束算法。

def bubbole_sort_1(li):
    for i in range(len(li)-1):
        exchange = False
        for j in range(len(li)-i-1):
            if li[j] > li[j+1]:
                li[j],li[j+1] = li[j+1],li[j]
                exchange = True
        if not exchange:
            return 

• 选择排序思路
  • 一趟遍历记录最小的数，放到第一个位置；
  • 再一趟遍历记录剩余列表中最小的数，继续放置；
  • ……
  • 问题是：怎么选出最小的数？
• 代码关键点：
  • 无序区
  • 最小数的位置
• 选择排序代码

def select_sort(li):
   for i in range(len(li) - 1):
      min_loc = i
      for j in range(i+1, len(li)):
        if li[j] < li[min_loc]:
            min_loc = j
      if min_loc != i:
        li[i], li[min_loc] = li[min_loc], li[i]

• 时间复杂度：O(n2)
• 插入排序思路
• 列表被分为有序区和无序区两个部分。最初有序区只有一个元素。
• 每次从无序区选择一个元素，插入到有序区的位置，直到无序区变空。
• 代码关键点：
• 摸到的牌
• 手里的牌

　　

　　

 def insert_sort(li):
     for i in range(1, len(li)):
         tmp = li[i]
         j = i - 1
         while j >= 0 and tmp < li[j]:
             li[j + 1] = li[j]
             j = j - 1
         li[j + 1] = tmp

代码

• 时间复杂度：O(n2)
• 优化空间：应用二分查找来寻找插入点（并没有什么卵用）

小结——排序LOW B三人组

• 冒泡排序 插入排序 选择排序
• 时间复杂度：O(n2)
• 空间复杂度：O(1)

快速排序

• 快速排序：快
  • 好写的排序算法里最快的
  • 快的排序算法里最好写的
• 快速排序思路　　

  • 取一个元素p（第一个元素），使元素p归位；

  • 列表被p分成两部分，左边都比p小，右边都比p大；

  • 递归完成排序。

　　　　

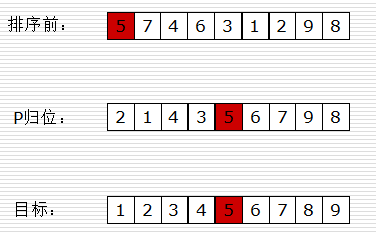
• 算法关键点：
  • 整理
  • 递归

 def quick_sort(data, left, right):
        if left < right:
            mid = partition(data, left, right)
            quick_sort(data, left, mid - 1)
            quick_sort(data, mid + 1, right)

快速排序代码——第一步

• 怎么写partition函数

　

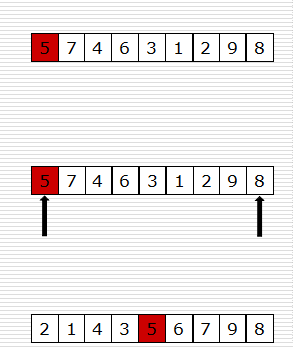
 def partition(data, left, right):
     tmp = data[left]
     while left < right:
         while left < right and data[right] >= tmp:
             right -= 1
         data[left] = data[right]
         while left < right and data[left] <= tmp:
             left += 1
         data[right] = data[left]
     data[left] = tmp
     return left

快速排序代码——第二步

还不理解partition函数？

def partition(data, left, right):
    tmp = data[left]
    while left < right:
        while left < right and data[right] >= tmp:
            right -= 1
        data[left] = data[right]
        while left < right and data[left] <= tmp:
            left += 1
        data[right] = data[left]
    data[left] = tmp
    return left

快速排序-如何

• 效率
  • 快速排序真的比冒泡排序快吗？
  • 为什么快了？
  • 快了多少？
• 问题
  • 最坏情况
  • 递归

快速排序-练习

• 如果想将列表进行降序排序，应该修改哪些符号？
• 还是对于刚才那个学生信息表，修改快速排序代码，使其能够进行排序。

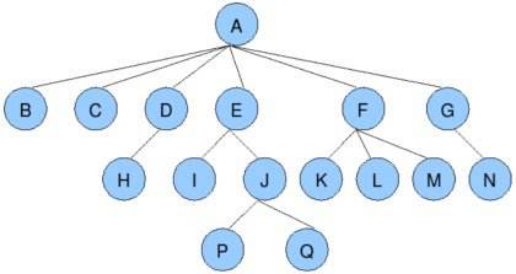
堆排序前传——树与二叉树简介

• 树是一种数据结构 比如：目录结构
• 树是一种可以递归定义的数据结构
• 树是由n个节点组成的集合：
  • 如果n=0，那这是一棵空树；
  • 如果n>0，那存在1个节点作为树的根节点，其他节点可以分为m个集合，每个集合本身又是一棵树。
• 一些概念
  • 根节点、叶子节点
  • 树的深度（高度）
  • 树的度
  • 孩子节点/父节点
  • 子树

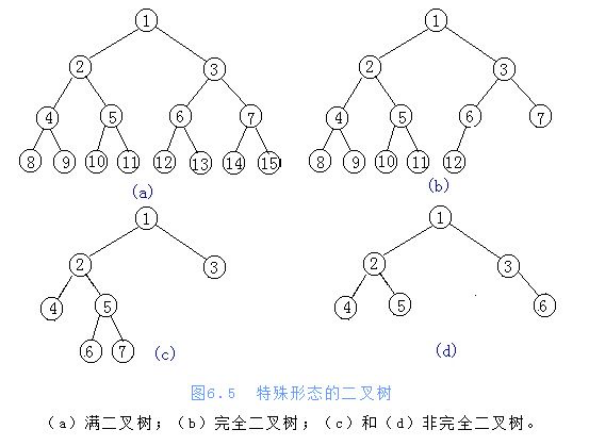
特殊且常用的树——二叉树

• 二叉树：度不超过2的树（节点最多有两个叉）

　　

• 两种特殊二叉树
  • 满二叉树
  • 完全二叉树

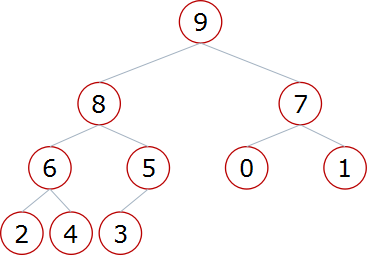
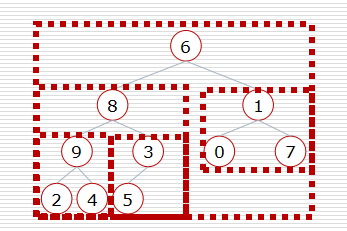
• 二叉树的存储方式

• • 链式存储方式
  • 顺序存储方式（列表）
• 父节点和左孩子节点的编号下标有什么关系？
  • 0-1 1-3 2-5 3-7 4-9

• • i – 2i+1

• 父节点和右孩子节点的编号下标有什么关系？
  • 0-2 1-4 2-6 3-8 4-10

  • i – 2i+2

• 比如，我们要找根节点左孩子的左孩子

二叉树小结

• 二叉树是度不超过2的树
• 满二叉树与完全二叉树
• （完全）二叉树可以用列表来存储，通过规律可以从父亲找到孩子或从孩子找到父亲

堆排序

• 堆
• 大根堆：一棵完全二叉树，满足任一节点都比其孩子节点大

　　　　　　　

　　

• 小根堆：一棵完全二叉树，满足任一节点都比其孩子节点小

　　　　　　

• 堆这个玩意…
  • 假设：节点的左右子树都是堆，但自身不是堆

　　　　　　

• • 当根节点的左右子树都是堆时，可以通过一次向下的调整来将其变换成一个堆。
• 堆排序过程

  • 建立堆

  • 得到堆顶元素，为最大元素

  • 去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序。

  • 堆顶元素为第二大元素。

  • 重复步骤3，直到堆变空。

• 构造堆

　　　　

• 挨个出数

　　

 def sift(data, low, high):
     i = low
     j = 2 * i + 1
     tmp = data[i]
     while j <= high:
         if j < high and data[j] < data[j + 1]:
             j += 1
         if tmp < data[j]:
             data[i] = data[j]
             i = j
             j = 2 * i + 1
         else:
             break
     data[i] = tmp

 def heap_sort(data):
     n = len(data)
     for i in range(n // 2 - 1, -1, -1):
         sift(data, i, n - 1)
     for i in range(n - 1, -1, -1):
         data[0], data[i] = data[i], data[0]
         sift(data, 0, i - 1)

堆排序代码

归并排序

• 假设现在的列表分两段有序，如何将其合成为一个有序列表

　　　　

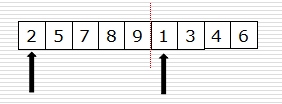
• 这种操作称为一次归并。

 def merge(li, low, mid, high):
     i = low
     j = mid + 1
     ltmp = []
     while i <= mid and j <= high:
         if li[i] <= li[j]:
             ltmp.append(li[i])
             i += 1
         else:
             ltmp.append(li[j])
             j += 1
     while i <= mid:
         ltmp.append(li[i])
         i += 1
     while j <= high:
         ltmp.append(li[j])
         j += 1
     li[low:high + 1] = ltmp

一次归并代码

有了归并怎么用？

• 分解：将列表越分越小，直至分成一个元素。
• 一个元素是有序的。
• 合并：将两个有序列表归并，列表越来越大。

def mergesort(li, low, high):
    if low < high:
        mid = (low + high) // 2
        mergesort(li, low, mid)
        mergesort(li, mid + 1, high)
        merge(li, low, mid, high)

归并排序

快速排序、堆排序、归并排序-小结

• 三种排序算法的时间复杂度都是O(nlogn)
• 一般情况下，就运行时间而言：
  • 快速排序 < 归并排序 < 堆排序
• 三种排序算法的缺点：
  • 快速排序：极端情况下排序效率低
  • 归并排序：需要额外的内存开销
  • 堆排序：在快的排序算法中相对较慢

希尔排序思路

• 希尔排序是一种分组插入排序算法。
• 首先取一个整数d1=n/2，将元素分为d1个组，每组相邻量元素之间距离为d1，在各组内进行直接插入排序；
• 取第二个整数d2=d1/2，重复上述分组排序过程，直到di=1，即所有元素在同一组内进行直接插入排序。

　　

• 希尔排序每趟并不使某些元素有序，而是使整体数据越来越接近有序；最后一趟排序使得所有数据有序。

 def shell_sort(li):
     gap = len(li) // 2
     while gap > 0:
         for i in range(gap, len(li)):
             tmp = li[i]
             j = i - gap
             while j >= 0 and tmp < li[j]:
                 li[j + gap] = li[j]
                 j -= gap
             li[j + gap] = tmp
         gap /= 2

希尔排序

排序-小结

　　

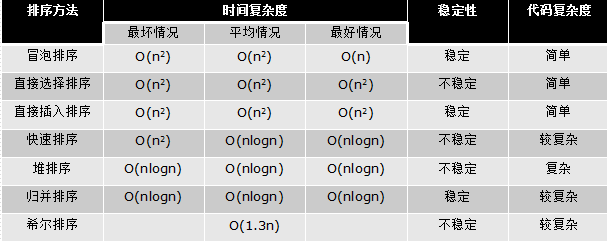
排序-赠品1

• 现在有一个列表，列表中的数范围都在0到100之间，列表长度大约为100万。设计算法在O(n)时间复杂度内将列表进行排序。
• 赠品1-计数排序

  • 创建一个列表，用来统计每个数出现的次数。

  • def count_sort(li, max_num):
        count = [0 for i in range(max_num + 1)]
        for num in li:
            count[num] += 1
        i = 0
        for num,m in enumerate(count):
            for j in range(m):
                li[i] = num
                i += 1

排序-赠品2

• 现在有n个数（n>10000），设计算法，按大小顺序得到前m大的数。
  • 应用场景：榜单TOP 10

赠品2-堆的应用（了解）

• 解决思路： 取列表前10个元素建立一个小根堆。堆顶就是目前第10大的数。
• 依次向后遍历原列表，对于列表中的元素，如果小于堆顶，则忽略该元素；如果大于堆顶，则将堆顶更换为该元素，并且对堆进行一次调整；
• 遍历列表所有元素后，倒序弹出堆顶。

　　

def topn(li, n):
    heap = li[0:n]
    # 建堆
    for i in range(n // 2 - 1, -1, -1):
        sift(heap, i, n - 1)
    # 遍历
    for i in range(n, len(li)):
        if li[i] > heap[0]:
            heap[0] = li[i]
            sift(heap, 0, n - 1)
    # 出数
    for i in range(n - 1, -1, -1):
        heap[0], heap[i] = heap[i], heap[0]
        sift(heap, 0, i - 1)

解决方案

赠品2-堆的应用（了解）

• 优先队列：一些元素的集合，POP操作每次执行都会从优先队列中弹出最大（或最小）的元素。
• 堆——优先队列
• Python内置模块——heapq 利用heapq模块实现堆排序

　　

• 利用heapq模块实现取top-k

  • heapq.nlargest(100, li)

算法-习题1

• 给定一个列表和一个整数，设计算法找到两个数的下标，使得两个数之和为给定的整数。保证肯定仅有一个结果。
• 例如，列表[1,2,5,4]与目标整数3，1+2=3，结果为(0, 1).
• https://leetcode.com/problems/two-sum/?tab=Description

算法-习题2

• 给定一个升序列表和一个整数，返回该整数在列表中的下标范围。
• 例如：列表[1,2,3,3,3,4,4,5]，若查找3，则返回(2,4)；若查找1，则返回(0,0)。
• https://leetcode.com/problems/search-for-a-range/description/