Reservoir Sampling - 蓄水池抽样算法&&及相关等概率问题

• 蓄水池抽样——《编程珠玑》读书笔记

• 382. Linked List Random Node

• 398. Random Pick Index

• 从n个数中随机选取m个

• 等概率随机函数面试题总结

        问题：如何随机从n个对象中选择一个对象，这n个对象是按序排列的，但是在此之前你是不知道n的值的。

 思路：如果我们知道n的值，那么问题就可以简单的用一个大随机数rand()%n得到一个确切的随机位置，那么该位置的对象就是所求的对象，选中的概率是1/n。

但现在我们并不知道n的值，这个问题便抽象为蓄水池抽样问题，即从一个包含n个对象的列表S中随机选取k个对象，n为一个非常大或者不知道的值。通常情况下，n是一个非常大的值，大到无法一次性把所有列表S中的对象都放到内存中。我们这个问题是蓄水池抽样问题的一个特例，即k=1。

解法：我们总是选择第一个对象，以1/2的概率选择第二个，以1/3的概率选择第三个，以此类推，以1/m的概率选择第m个对象。当该过程结束时，每一个对象具有相同的选中概率，即1/n，证明如下。

证明：第m个对象最终被选中的概率P=选择m的概率*其后面所有对象不被选择的概率，即

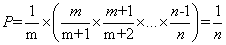
对应蓄水池抽样问题，可以类似的思路解决。先把读到的前k个对象放入“水库”，对于第k+1个对象开始，以k/(k+1)的概率选择该对象，以k/(k+2)的概率选择第k+2个对象，以此类推，以k/m的概率选择第m个对象（m>k）。如果m被选中，则随机替换水库中的一个对象。最终每个对象被选中的概率均为k/n，证明如下。

证明：第m个对象被选中的概率=选择m的概率*（其后元素不被选择的概率+其后元素被选择的概率*不替换第m个对象的概率），即