BZOJ1001 BeiJing2006 狼抓兔子 【网络流-最小割】*

BZOJ1001 BeiJing2006 狼抓兔子

---

Description

现在小朋友们最喜欢的”喜羊羊与灰太狼”,话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：



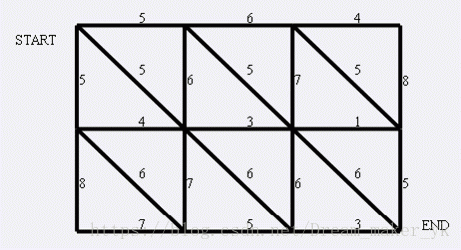
左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路

1:(x,y)<==>(x+1,y)

2:(x,y)<==>(x,y+1)

3:(x,y)<==>(x+1,y+1)

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦.

Input

第一行为N,M.表示网格的大小，N,M均小于等于1000.

接下来分三部分

第一部分共N行，每行M-1个数，表示横向道路的权值.

第二部分共N-1行，每行M个数，表示纵向道路的权值.

第三部分共N-1行，每行M-1个数，表示斜向道路的权值.

输入文件保证不超过10M

Output

输出一个整数，表示参与伏击的狼的最小数量.

Sample Input

3 4

5 6 4

4 3 1

7 5 3

5 6 7 8

8 7 6 5

5 5 5

6 6 6

Sample Output

14

HINT

2015.4.16新加数据一组，可能会卡掉从前可以过的程序。

---

最小割模型还是挺好看出来的

然后转化成最大流，但我不知道为什么又是MLE又是TLE。。

然后网上到说如果dinic在DFS的时候flow为0就可以直接把这个点的d值设为0，确实可以极大程度的优化时间

然后注意一下这个是无向图，正边和反边的cap都应该设成cap值

挺好的一道题

---

#include<bits/stdc++.h>
using namespace std;
#define N 1000001
#define INF 0x3f3f3f3f
struct Edge{int v,next,cap,flow;};
struct Dinic{
    int s,t,tot,vis[N],d[N];
    Edge E[N*6];int head[N];
    Dinic(){tot=1;}
    void add(int u,int v,int cap){
        E[++tot]=((Edge){v,head[u],cap,0});head[u]=tot;
        E[++tot]=((Edge){u,head[v],cap,0});head[v]=tot;//*******
    }
    bool bfs(){
        memset(vis,0,sizeof(vis));
        memset(d,0,sizeof(d));
        queue<int> Q;
        Q.push(s);
        vis[s]=1;
        while(!Q.empty()){
            int u=Q.front();Q.pop();
            for(int i=head[u];i;i=E[i].next){
                if(!vis[E[i].v]&&E[i].cap>E[i].flow){
                    vis[E[i].v]=1;
                    d[E[i].v]=d[u]+1;
                    Q.push(E[i].v);
                }
            }
        }
        return vis[t];
    }
    int dfs(int u,int a){
        if(u==t||!a)return a;
        int flow=0;
        for(int i=head[u];i;i=E[i].next){
            if(d[E[i].v]!=d[u]+1)continue;
            int f=dfs(E[i].v,min(E[i].cap-E[i].flow,a));
            if(!f)continue;
            E[i].flow+=f;
            E[i^1].flow-=f;
            flow+=f;
            a-=f;
            if(!a)return flow;
        }
        if(!flow)d[u]=0;//*************
        return flow;
    }
    int Maxflow(){
        int flow=0;
        while(bfs())flow+=dfs(s,INF);
        return flow;
    }
}dinic;
int n,m,cap;
int getind(int x,int y){return (x-1)*m+y;}
int main(){
    scanf("%d%d",&n,&m);
    dinic.s=1;dinic.t=n*m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<m;j++){
            scanf("%d",&cap);
            dinic.add(getind(i,j),getind(i,j+1),cap);
        }
    for(int i=1;i<n;i++)
        for(int j=1;j<=m;j++){
            scanf("%d",&cap);
            dinic.add(getind(i,j),getind(i+1,j),cap);
        }
    for(int i=1;i<n;i++)
        for(int j=1;j<m;j++){
            scanf("%d",&cap);
            dinic.add(getind(i,j),getind(i+1,j+1),cap);
        }
    printf("%d",dinic.Maxflow());
    return 0;
}