AVL树 - 学习笔记

2017-08-29 14:35:55

writer：pprp

AVL树就是带有平衡条件的二叉查找树。每个节点的左子树和右子树高度相差最多为1的二叉查找树

空树的高度定为-1

对树的修正称为旋转

对内部的来说是双旋，对外部的调整修正是单旋

----------------------------------------------------------------------------------------------------------------

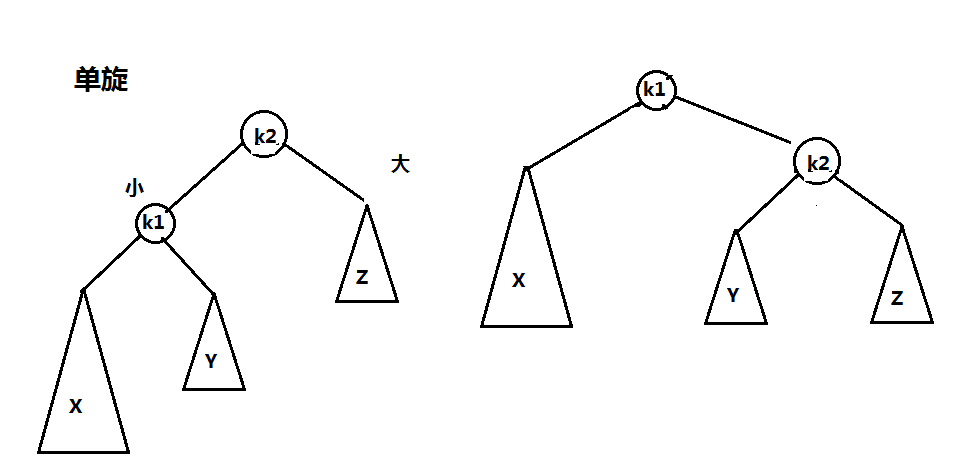
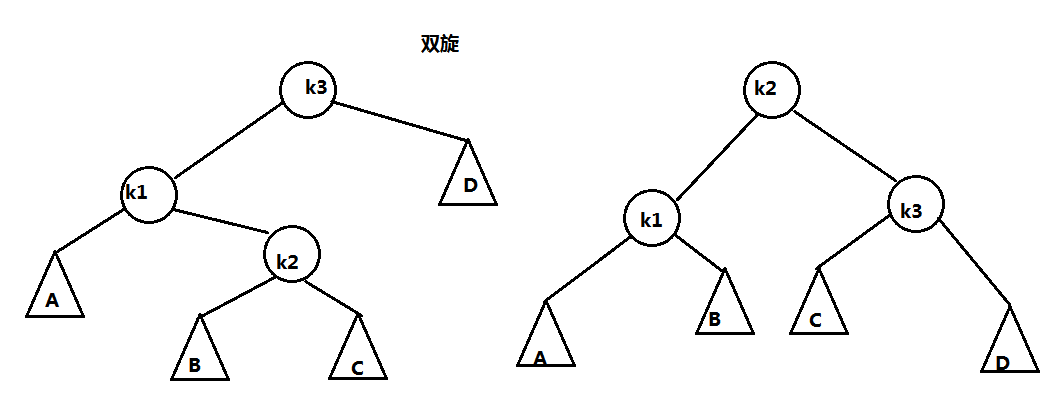
由于一次旋转总能解决问题，因此编写非递归程序要比编写递归程序快很多，但是非递归方式编写比较难

还是很多人都选择递归的方式，这里也选择递归的方式，比较容易理解；

代码如下：（还没有完全写好，删除部分不太理解）

/*
@theme:AVL tree
@writer:pprp
@begin:14:32
@end:16:26
@declare:带有平衡条件的二叉查找树,这里不需要一个创建节点的函数，
因为相关操作已经在Insert函数中完成了
@date:2017/8/29
*/

#include <bits/stdc++.h>

using namespace std;
struct AvlNode;
typedef struct AvlNode* Position;
typedef struct AvlNode* AvlTree;

AvlTree MakeEmpty(AvlTree T);
Position Find(int X, AvlTree T);
Position FindMin(AvlTree T);
Position FindMax(AvlTree T);
AvlTree Insert(int X, AvlTree T);
AvlTree Delete(int X, AvlTree T);

static Position SingleRotateWithLeft(Position);
static Position DoubleRotateWithLeft(Position);
static Position SingleRotateWithRight(Position);
static Position DoubleRotateWithRight(Position);

//AVL tree节点声明
struct AvlNode
{
    int element;
    AvlTree left;
    AvlTree right;
    int Height;
};

//一个快速的函数来返回节点高度
static int Height(Position P)
{
    if(P == NULL)
        return -;
    else
        return P->Height;
}

//向AVL树中插入节点的函数
AvlTree Insert(int X, AvlTree T)
{
    //如果节点为空，建立然后返回一个单节点的树
    if(T == NULL)
    {
        T = new AvlNode();
        //如果失败
        if(T == NULL)
        {
            cout << "Out of place！" << endl;
        }
        else
        {
            T->element = X;
            T->Height = ;
            T->left = T->right = NULL;
        }
    }
    else if(X < T->element) //如果头结点不为空
    {
        T->left = Insert(X,T->left);
        //question
        //如果不满足AVL tree的要求了，且左侧高于右侧，对左侧进行处理
        if(Height(T->left) - Height(T->right) == )
        {
            if(X < T->left->element)//如果小于左边
                T = SingleRotateWithLeft(T);//进行左侧的单旋
            else
                T = DoubleRotateWithLeft(T);//进行左侧的双旋
        }
    }
    else if(X > T->element)
    {
        T->right = Insert(X, T->right);
        //如果右侧高于左侧进行旋转
        if(Height(T->right) - Height(T->left) == )
        {
            if(X > T->right->element)
                T = SingleRotateWithRight(T);
            else
                T =  DoubleRotateWithRight(T);
        }
    }
    //else X is in the tree already , we'll do nothing
    T->Height = max(Height(T->left),Height(T->right)) + ;
    return T;
}

//执行单旋转的左边 LL
static Position SingleRotateWithLeft(Position K2)
{
    Position K1;
    K1 = K2->left;
    K2->left = K1->right;
    K1->right = K2;

    K2->Height = max(Height(K2->left),Height(K2->right))+;
    K1->Height = max(Height(K1->left),Height(K1->right))+;

    return K1;
}

//执行双旋转的左边 LR
static Position DoubleRotateWithLeft(Position K3)
{
    //rotate between K1 and K2
    K3->left = SingleRotateWithRight(K3->left);
    //rotate between K3 and K2
    return SingleRotateWithLeft(K3);
}

//执行单旋转的右边 RR
static Position SingleRotateWithRight(Position K1)
{
    Position K2;

    K2 = K1->left;
    K1->left = K2->right;
    K2->right = K1;

    K1->Height = max(Height(K1->right),Height(K2->left))+;
    K2->Height = max(Height(K2->right),Height(K2->left))+;

    return K2;
}
//执行双旋转的右边 RL
static Position DoubleRotateWithRight(Position K3)
{
    K3->right = SingleRotateWithLeft(K3->right);
    return SingleRotateWithRight(K3);
}

//进行中序遍历
void MidPrint(AvlTree T)
{
    if(T != NULL)
    {
        MidPrint(T->left);
        cout << T->element << " ";
        MidPrint(T->right);
    }
}

//查找函数，返回一个指针
Position Find(int X, AvlTree T)
{
    if(T == NULL)
        return NULL;
    if(X < T->element)
        return Find(X, T->right);
    else if(X > T->element)
        return Find(X, T->left);
    else
        return T;
}

//找到最大值
Position FindMax(AvlTree T)
{
    if(T == NULL)
        return NULL;
    else if(T->right == NULL)
        return T;
    else
        return FindMax(T->right);
}

//找到最小值
Position FindMin(AvlTree T)
{
    if(T == NULL)
        return NULL;
    else if(T->left == NULL)
        return T;
    else
        return FindMin(T->left);
}

//删除节点，返回根节点
AvlTree Delete(int X, AvlTree T)
{
    AvlTree tmp = Find(X,T);
    if(T == NULL || tmp == NULL)
        return NULL;
    if(X < T->element)//如果在左子树中
    {
        T->left = Delete(X,T->left);
        //开始调整由于删除带来的影响
        if(Height(T->right) - Height(T->left) == )
        {
            AvlTree K = T->right;//因为右边高度比较高
            if(Height(K->left) > Height(K->right))
                DoubleRotateWithRight(T);
            else
                SingleRotateWithRight(T);
        }
    }
    else if(X > T->element) //如果在右子树中
    {
        T->right = Delete(X,T->right);
        if(Height(T->left) - Height(T->right) == )
        {
            AvlTree K = T->left;
            if(Height(K->right) > Height(K->left))
                DoubleRotateWithLeft(T);
            else
                SingleRotateWithLeft(T);
        }
    }
    else if(X == T->element)
    {
        // 如果两个孩子非空
        if(T->left && T->right)
        {
            //维护AVL树特性:本来可以选择两种方式进行删除
            //现在要优先删除高度比较高的子树
            if(Height(T->left) > Height(T->right))
            {
                AvlTree Max = FindMax(T->left); //找到最大值
                T->element = Max->element;   //将内容进行替换
                delete(Max); //删除该节点
                Max = NULL;
            }
            else
            {
                AvlTree Min = FindMin(T->right);
                T->element = Min->element;
                delete(Min);//删除该节点
                Min = NULL;
            }
        }
        else //如果有一个子节点或者没有子节点
        {
            AvlTree tmp = T;
            T = T->left == NULL ? T->right:T->left;
            delete(tmp);
        }
    }
    return T;
}

//清空整个树
AvlTree MakeEmpty(AvlTree T)
{
    if(T!= NULL)
    {
        MakeEmpty(T->right);
        MakeEmpty(T->left);
        delete(T);
    }
}

int main()
{

    AvlTree T;
    int n, tmp;
    cin >> n;
    for(int i =  ; i < n ; i++)
    {
        cin >> tmp;
        T = Insert(tmp,T);
    }

    return ;
}