SPOJ:[DIVCNT3]Counting Divisors

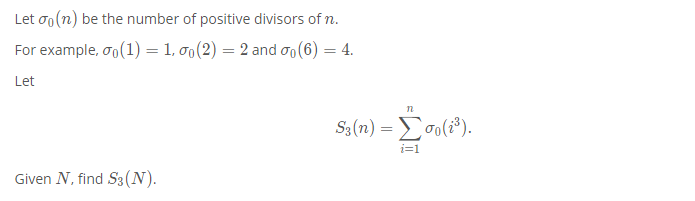
题目大意：求1~N的每个数因子数的立方和。

题解：由于N过大，我们不能直接通过线性筛求解。我们可以采用洲阁筛。

洲阁筛的式子可以写成：

对于F(1~√n)，可以直接线性筛求解。

对于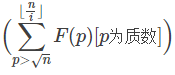，我们进行以下DP：

g[i][j]为1~j中，与前i个质数互质的数的F值之和。

dp过程中，有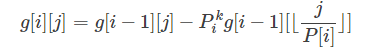

如果p[i]>j，则g[i][j]=F(1)；

如果p[i]*p[i]>j>=p[i]，则g[i][j]=g[i-1][j]-p[i]^k*F(1)=g[d][j]-(p[d+1]^k~p[i]^k)*F(1)，其中p[d]为最大的p[d]*p[d]<=j的质数；

如果j>=p[i]*p[i]，我们老老实实调用式子。

对于，我们用类似的方式DP：

f[i][j]为1~j中，只以第i个到第m个质数为质因子的数的F值之和（m为√N以内质数个数）。

类似的，dp过程中，有

如果p[i]>j，则f[i][j]=F(1)；

如果p[i]*p[i]>j>=p[i]，则f[i][j]=f[i+1][j]+F(p[i])*F(1)=F(1)+F(p[i]~p[e])*F(1)，其中p[e]为最大的p[e]<=j的质数；

如果j>=p[i]*p[i]，我们老老实实调用式子。

代码：

 #include<bits/stdc++.h>
 using namespace std;
 long long block,n,lb[],dp[],zs[],ans[],ans2;
 bool bo[],bo2[];
 int dp2[],dp3[],m,mm,tot,j,bo3[],tt;
 void xxs(int n)
 {
     ans[]=;
     for(int i=;i<=n;i++)
     {
         if(bo[i]==){ mm++; zs[mm]=i; ans[i]=; bo2[i]=; bo3[i]=; }
         for(int j=;j<=mm;j++)
         if(zs[j]*i>n)break;else
         if(i%zs[j]==)
         {
             if(bo2[i]==)bo2[i*zs[j]]=; bo3[i*zs[j]]=bo3[i]+; ans[i*zs[j]]=ans[i]/bo3[i]*(bo3[i]+);
             bo[i*zs[j]]=; break;
         }else { ans[i*zs[j]]=ans[i]*; bo[i*zs[j]]=; bo3[i*zs[j]]=; }
     }
 }
 int dy(long long x){ if(x<=block)return x;else return tot-n/x+; }
 long long get(int i,int j)
 {
     if(dp2[j]==i)return dp[j];else
     if(lb[j]<zs[i]){ if(j>)return ; return ; }
     return dp[j]-i+dp2[j];
 }
 long long get2(int i,int j)
 {
     if(dp2[j]==i)return dp[j];else
     if(lb[j]<zs[i])return ;
     return (dp3[j]-i+)*+;
 }
 int main()
 {
     scanf("%d",&tt); xxs();
     for(int ii=;ii<=tt;ii++)
     {
         scanf("%lld",&n); block=(int)sqrt(n); ans2=;
         for(m=;m<=mm;m++)if(zs[m]>block)break; m--; tot=;
         for(int i=;i<=block;i++){ lb[++tot]=i; if(1ll*i*i<n)lb[++tot]=n/i; }
         sort(lb+,lb+tot+);
         for(int i=;i<=tot;i++)dp[i]=lb[i],dp2[i]=;
         for(int i=;i<=m;i++)
         {
             for(int j=tot;j>=;j--)
             {
                 if(lb[j]<zs[i]*zs[i])break; dp2[j]=i;
                 dp[j]=dp[j]-get(i-,dy(lb[j]/zs[i]));
             }
         }
         for(int i=;i<=block;i++)
         ans2=ans2+ans[i]*(get(m,tot-i+)-)*;
         j=;
         for(int i=;i<=tot;i++)
         {
             dp[i]=; dp2[i]=m+;
             while((j<=m)and(zs[j]<=lb[i]))j++; dp3[i]=j-;
         }
         for(int i=m;i>=;i--)
         {
             for(int j=tot;j>=;j--)
             {
                 if(lb[j]<zs[i]*zs[i])break; dp[j]=get2(i+,j); dp2[j]=i;
                 long long t=j,l=;
                 while(lb[t]>=zs[i])
                 {
                     t=dy(lb[t]/zs[i]); l+=;
                     dp[j]=dp[j]+l*get2(i+,t);
                 }
             }
         }
         ans2=ans2+get2(,tot);
         printf("%lld\n",ans2);
     }
 }