【算法】——递归：小白正在上楼梯，楼梯有n阶台阶，小白一次可以上1阶，2阶或者3阶，实现一个方法，计算小白有多少种走完楼梯的方式。

分析：从最后一步分析，能有的情况有三种情况构成，写出如图所示的方程

//和斐波拉契相似
int void f(int n)
{
    //考虑出口
    if(n==) return ;//正常思路是返回0
    if(n==) return ;//通过自己想可以得出只有1种方式
    if(n==) return ;//通过自己想可以得到只有2种方法
    return f(n-)+f(n-)+f(n-);//递归计算
  }  

　但是在验算的时候发现当n=3的时候，结果为f(2)+f(1)+f(0)=3；不符合，通过思考应该是4种，所以把n==0时返回1

验算思路如图所示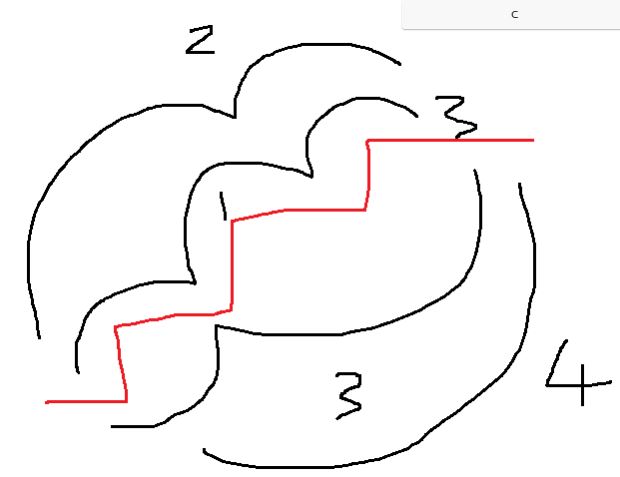

最终代码：

//和斐波拉契相似
int void f(int n)
{
    //考虑出口
    if(n==) return ;//正常思路是返回0
    if(n==) return ;//通过自己想可以得出只有1种方式
    if(n==) return ;//通过自己想可以得到只有2种方法
    return f(n-)+f(n-)+f(n-);//递归计算
    //但是在验算的时候发现当n=3的时候，结果为f(2)+f(1)+f(0)=3；不符合，通过思考应该是4种，所以把n==0时返回1
  }