机器学习作业（八）异常检测与推荐系统——Matlab实现

题目下载【传送门】

第1题

简述：对于一组网络数据进行异常检测.

第1步：读取数据文件，使用高斯分布计算 μ 和 σ²：

%  The following command loads the dataset. You should now have the
%  variables X, Xval, yval in your environment
load('ex8data1.mat');
 
%  Estimate my and sigma2
[mu sigma2] = estimateGaussian(X);

其中高斯分布计算函数estimateGaussian：

function [mu sigma2] = estimateGaussian(X)
 
% Useful variables
[m, n] = size(X);
 
% You should return these values correctly
mu = zeros(n, 1);
sigma2 = zeros(n, 1);
 
mu = mean(X);
sigma2 = var(X, 1);
% mu = mu';
% sigma2 = sigma2';
 
end

第2步：计算概率p(x)：

%  Returns the density of the multivariate normal at each data point (row)
%  of X
p = multivariateGaussian(X, mu, sigma2);

其中概率计算函数

function p = multivariateGaussian(X, mu, Sigma2)
 
k = length(mu);
 
if (size(Sigma2, 2) == 1) || (size(Sigma2, 1) == 1)
    Sigma2 = diag(Sigma2);
end
 
X = bsxfun(@minus, X, mu(:)');
p = (2 * pi) ^ (- k / 2) * det(Sigma2) ^ (-0.5) * ...
    exp(-0.5 * sum(bsxfun(@times, X * pinv(Sigma2), X), 2));
 
end

第3步：可视化数据，并绘制概率等高线：

%  Visualize the fit
visualizeFit(X,  mu, sigma2);
xlabel('Latency (ms)');
ylabel('Throughput (mb/s)');

其中visualizeFit函数：

function visualizeFit(X, mu, sigma2)
 
[X1,X2] = meshgrid(0:.5:35);
Z = multivariateGaussian([X1(:) X2(:)],mu,sigma2);
Z = reshape(Z,size(X1));
 
plot(X(:, 1), X(:, 2),'bx');
hold on;
% Do not plot if there are infinities
if (sum(isinf(Z)) == 0)
    contour(X1, X2, Z, 10.^(-20:3:0)');
end
hold off;
 
end

运行结果：

第4步：使用交叉验证集选出最佳参数 ε：

pval = multivariateGaussian(Xval, mu, sigma2);
 
[epsilon F1] = selectThreshold(yval, pval);
fprintf('Best epsilon found using cross-validation: %e\n', epsilon);
fprintf('Best F1 on Cross Validation Set:  %f\n', F1);

其中selectThreshold函数：

function [bestEpsilon bestF1] = selectThreshold(yval, pval)
 
bestEpsilon = 0;
bestF1 = 0;
F1 = 0;
 
stepsize = (max(pval) - min(pval)) / 1000;
for epsilon = min(pval):stepsize:max(pval)
    predictions = pval < epsilon;
    tp = sum(predictions .* yval);
    prec = tp / sum(predictions);
    rec = tp / sum(yval);
    F1 = 2 * prec * rec / (prec + rec);
 
    if F1 > bestF1
       bestF1 = F1;
       bestEpsilon = epsilon;
    end
end
 
end

运行结果：

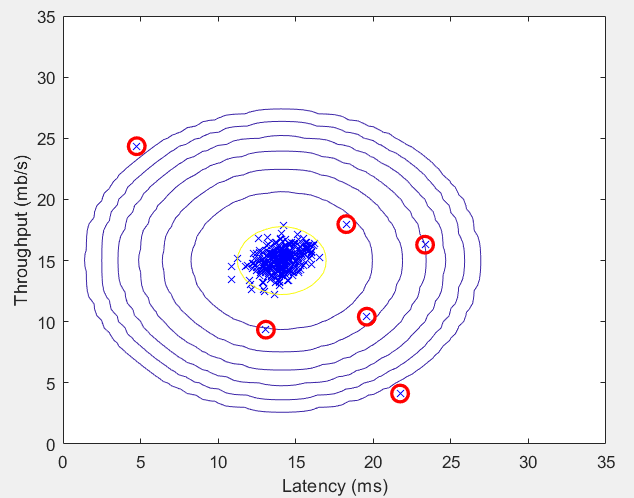
第5步：找出异常点，并可视化标记：

%  Find the outliers in the training set and plot the
outliers = find(p < epsilon);
 
%  Draw a red circle around those outliers
hold on
plot(X(outliers, 1), X(outliers, 2), 'ro', 'LineWidth', 2, 'MarkerSize', 10);
hold off

运行结果：

第2题

简述：实现电影推荐系统

第1步：读取数据文件(截取较少的数据)：

%  Load data
load ('ex8_movies.mat');
 
%  Y is a 1682x943 matrix, containing ratings (1-5) of 1682 movies on
%  943 users
%
%  R is a 1682x943 matrix, where R(i,j) = 1 if and only if user j gave a
%  rating to movie i
 
%  Load pre-trained weights (X, Theta, num_users, num_movies, num_features)
load ('ex8_movieParams.mat');
 
%  Reduce the data set size so that this runs faster
num_users = 4; num_movies = 5; num_features = 3;
X = X(1:num_movies, 1:num_features);
Theta = Theta(1:num_users, 1:num_features);
Y = Y(1:num_movies, 1:num_users);
R = R(1:num_movies, 1:num_users);

第2步：计算代价函数和梯度：

J = cofiCostFunc([X(:) ; Theta(:)], Y, R, num_users, num_movies, ...
               num_features, 1.5);

其中cofiCostFunc函数：

function [J, grad] = cofiCostFunc(params, Y, R, num_users, num_movies, ...
                                  num_features, lambda)
 
% Unfold the U and W matrices from params
X = reshape(params(1:num_movies*num_features), num_movies, num_features);
Theta = reshape(params(num_movies*num_features+1:end), ...
                num_users, num_features);
 
% You need to return the following values correctly
J = 0;
X_grad = zeros(size(X));
Theta_grad = zeros(size(Theta));
 
cost = (X * Theta' - Y) .* R;
J = 1 / 2 * sum(sum(cost .^ 2));
J = J + lambda / 2 * (sum(sum(Theta .^ 2)) + sum(sum(X .^ 2)));
 
X_grad = cost * Theta;
X_grad = X_grad + lambda * X;
 
Theta_grad = X' * cost;
Theta_grad = Theta_grad' + lambda * Theta;
 
grad = [X_grad(:); Theta_grad(:)];
 
end

第3步：进行梯度检测：

%  Check gradients by running checkNNGradients
checkCostFunction(1.5);

其中checkCostFunction函数：

function checkCostFunction(lambda)
 
% Set lambda
if ~exist('lambda', 'var') || isempty(lambda)
    lambda = 0;
end
 
%% Create small problem
X_t = rand(4, 3);
Theta_t = rand(5, 3);
 
% Zap out most entries
Y = X_t * Theta_t';
Y(rand(size(Y)) > 0.5) = 0;
R = zeros(size(Y));
R(Y ~= 0) = 1;
 
%% Run Gradient Checking
X = randn(size(X_t));
Theta = randn(size(Theta_t));
num_users = size(Y, 2);
num_movies = size(Y, 1);
num_features = size(Theta_t, 2);
 
numgrad = computeNumericalGradient( ...
                @(t) cofiCostFunc(t, Y, R, num_users, num_movies, ...
                                num_features, lambda), [X(:); Theta(:)]);
 
[cost, grad] = cofiCostFunc([X(:); Theta(:)],  Y, R, num_users, ...
                          num_movies, num_features, lambda);
 
disp([numgrad grad]);
fprintf(['The above two columns you get should be very similar.\n' ...
         '(Left-Your Numerical Gradient, Right-Analytical Gradient)\n\n']);
 
diff = norm(numgrad-grad)/norm(numgrad+grad);
fprintf(['If your cost function implementation is correct, then \n' ...
         'the relative difference will be small (less than 1e-9). \n' ...
         '\nRelative Difference: %g\n'], diff);
 
end

其中computeNumericalGradient函数：

function numgrad = computeNumericalGradient(J, theta)            
 
numgrad = zeros(size(theta));
perturb = zeros(size(theta));
e = 1e-4;
for p = 1:numel(theta)
    % Set perturbation vector
    perturb(p) = e;
    loss1 = J(theta - perturb);
    loss2 = J(theta + perturb);
    % Compute Numerical Gradient
    numgrad(p) = (loss2 - loss1) / (2*e);
    perturb(p) = 0;
end
 
end

　　

第4步：对某一用户进行预测，初始化用户的信息：

movieList = loadMovieList();
 
%  Initialize my ratings
my_ratings = zeros(1682, 1);
 
my_ratings(1) = 4;
my_ratings(98) = 2;
my_ratings(7) = 3;
my_ratings(12)= 5;
my_ratings(54) = 4;
my_ratings(64)= 5;
my_ratings(66)= 3;
my_ratings(69) = 5;
my_ratings(183) = 4;
my_ratings(226) = 5;
my_ratings(355)= 5;

其中loadMovieList函数：

function movieList = loadMovieList()
 
%% Read the fixed movieulary list
fid = fopen('movie_ids.txt');
 
% Store all movies in cell array movie{}
n = 1682;  % Total number of movies 
 
movieList = cell(n, 1);
for i = 1:n
    % Read line
    line = fgets(fid);
    % Word Index (can ignore since it will be = i)
    [idx, movieName] = strtok(line, ' ');
    % Actual Word
    movieList{i} = strtrim(movieName);
end
fclose(fid);
 
end

第5步：将新用户增加到数据集中：

%  Load data
load('ex8_movies.mat');
 
%  Y is a 1682x943 matrix, containing ratings (1-5) of 1682 movies by
%  943 users
%
%  R is a 1682x943 matrix, where R(i,j) = 1 if and only if user j gave a
%  rating to movie i
 
%  Add our own ratings to the data matrix
Y = [my_ratings Y];
R = [(my_ratings ~= 0) R];

第6步：均值归一化：

%  Normalize Ratings
[Ynorm, Ymean] = normalizeRatings(Y, R);

其中normalizeRatings函数：

function [Ynorm, Ymean] = normalizeRatings(Y, R)
 
[m, n] = size(Y);
Ymean = zeros(m, 1);
Ynorm = zeros(size(Y));
for i = 1:m
    idx = find(R(i, :) == 1);
    Ymean(i) = mean(Y(i, idx));
    Ynorm(i, idx) = Y(i, idx) - Ymean(i);
end
 
end

第7步：实现梯度下降，训练模型：

%  Useful Values
num_users = size(Y, 2);
num_movies = size(Y, 1);
num_features = 10;
 
% Set Initial Parameters (Theta, X)
X = randn(num_movies, num_features);
Theta = randn(num_users, num_features);
 
initial_parameters = [X(:); Theta(:)];
 
% Set options for fmincg
options = optimset('GradObj', 'on', 'MaxIter', 100);
 
% Set Regularization
lambda = 10;
theta = fmincg (@(t)(cofiCostFunc(t, Ynorm, R, num_users, num_movies, ...
                                num_features, lambda)), ...
                initial_parameters, options);
 
% Unfold the returned theta back into U and W
X = reshape(theta(1:num_movies*num_features), num_movies, num_features);
Theta = reshape(theta(num_movies*num_features+1:end), ...
                num_users, num_features);

第8步：实现推荐功能：

p = X * Theta';
my_predictions = p(:,1) + Ymean;
 
movieList = loadMovieList();
 
[r, ix] = sort(my_predictions, 'descend');
fprintf('\nTop recommendations for you:\n');
for i=1:10
    j = ix(i);
    fprintf('Predicting rating %.1f for movie %s\n', my_predictions(j), ...
            movieList{j});
end

运行结果：