P1268 树的重量【构造】

题目描述

树可以用来表示物种之间的进化关系。一棵“进化树”是一个带边权的树，其叶节点表示一个物种，两个叶节点之间的距离表示两个物种的差异。现在，一个重要的问题是，根据物种之间的距离，重构相应的“进化树”。

令N={1..n}，用一个N上的矩阵M来定义树T。其中，矩阵M满足：对于任意的i，j，k，有M[i,j] + M[j,k] >= M[i,k]。树T满足：

1．叶节点属于集合N；

2．边权均为非负整数；

3．dT(i,j)=M[i,j]，其中dT(i,j)表示树上i到j的最短路径长度。

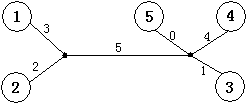
如下图，矩阵M描述了一棵树。

树的重量是指树上所有边权之和。对于任意给出的合法矩阵M，它所能表示树的重量是惟一确定的，不可能找到两棵不同重量的树，它们都符合矩阵M。你的任务就是，根据给出的矩阵M，计算M所表示树的重量。下图是上面给出的矩阵M所能表示的一棵树，这棵树的总重量为15。

输入格式

输入数据包含若干组数据。每组数据的第一行是一个整数n(2<n<30)。其后n-1行，给出的是矩阵M的一个上三角(不包含对角线)，矩阵中所有元素是不超过100的非负整数。输入数据保证合法。

输入数据以n=0结尾。

输出格式

对于每组输入，输出一行，一个整数，表示树的重量。

输入输出样例

输入 #1

5
5 9 12 8
8 11 7
5 1
4
4
15 36 60
31 55
36
0

输出 #1

15
71
 
和Three Paths on a tree类似地构造一个树上最短路的式子
把整张图看作一张AOE网

通过这张网来建立一棵树，具体实现操作是：
1、把一个为入树的点入树
2、在已经入树的它的邻接点中遍历来更新把这个点入树的最小花费。

显然此时花费是 (dis[i][k] + dis[j][k] - dis[i][j]) / 2;

3、树的总重量加上把这个点入树的最小花费

CODE

 #include <bits/stdc++.h>
 #define dbg(x) cout << #x << "=" << x << endl
 #define eps 1e-8
 #define pi acos(-1.0)
 
 using namespace std;
 typedef long long LL;
 
 template<class T>inline void read(T &res)
 {
     char c;T flag=;
     while((c=getchar())<''||c>'')if(c=='-')flag=-;res=c-'';
     while((c=getchar())>=''&&c<='')res=res*+c-'';res*=flag;
 }
 
 namespace _buff {
     const size_t BUFF =  << ;
     char ibuf[BUFF], *ib = ibuf, *ie = ibuf;
     char getc() {
         if (ib == ie) {
             ib = ibuf;
             ie = ibuf + fread(ibuf, , BUFF, stdin);
         }
         return ib == ie ? - : *ib++;
     }
 }
 
 int qread() {
     using namespace _buff;
     int ret = ;
     bool pos = true;
     char c = getc();
     for (; (c < '' || c > '') && c != '-'; c = getc()) {
         assert(~c);
     }
     if (c == '-') {
         pos = false;
         c = getc();
     }
     for (; c >= '' && c <= ''; c = getc()) {
         ret = (ret << ) + (ret << ) + (c ^ );
     }
     return pos ? ret : -ret;
 }
 
 const int maxn = ;
 
 int dis[maxn][maxn];
 int n;
 
 int main()
 {
     while(scanf("%d",&n) && n) {
         memset(dis, , sizeof(dis));
         for ( int i = ; i <= n; ++i ) {
             for ( int j = i+; j <= n; ++j ) {
                 read(dis[i][j]);
                 dis[j][i] = dis[i][j];
             }
         }
         int weight = ;
         int v = ;
         for ( int i = ; i <= n; ++i ) {
             int cost = 0x3f3f3f3f;
             for ( int j = ; j < i; ++j ) {
                 int temp = dis[i][v] + dis[i][j] - dis[v][j];
                 cost = min(cost, temp / );
                 //dbg(cost);
             }
             if(cost != 0x3f3f3f3f)
                 weight += cost;
         }
         cout << weight << endl;
     }
     return ;
 }