【math】梯度下降法(梯度下降法，牛顿法，高斯牛顿法，Levenberg-Marquardt算法)

原文：http://blog.csdn.net/dsbatigol/article/details/12448627

何为梯度？

一般解释：

f(x)在x0的梯度：就是f(x)变化最快的方向

举个例子，f()是一座山，站在半山腰，

往x方向走1米，高度上升0.4米，也就是说x方向上的偏导是 0.4

往y方向走1米，高度上升0.3米，也就是说y方向上的偏导是 0.3

这样梯度方向就是 (0.4 , 0.3)，也就是往这个方向走1米，所上升的高度最高。

(1*0.4/0.5)*0.4 +(1*0.3/0.5)*0.3 = 1*(0.3^2+0.4^2) = 0.5

这里使用了勾股定理的前提是走的距离足够小，因为走的距离足够小的时候，连续的曲面就看做一个平面，当然可以使用勾股定理。这里说距离1米是为了简便。

往x方向走1米，高度上升0.4米，也就是说x方向上的偏导是  0.4。

往y方向走1米，高度下降0.3米，也就是说y方向上的偏导是 -0.3 ，也就是说沿着 -y轴方向是上升的。

这样梯度方向就是 (0.4 , -0.3)，想象一下，是位于坐标轴的第四象限，这时沿着x和-y轴的分量都会上升。

和上面的情况一样，距离仍然是 0.5

所以，梯度不仅仅是f(x)在某一点变化最快的方向，而且是上升最快的方向，就如同室内温度的例子中是温度上升最快的方向。

梯度下降法：

由上面的讨论可以知道，梯度是上升最快的方向，那么如果我想下山，下降最快的方向呢，当然是逆着梯度了（将一点附近的曲面近似为平面），这就是梯度下降法，由于是逆着梯度，下降最快，又叫最速下降法。

迭代公式：

r是步长。

牛顿法：

（部分借鉴了：http://blog.csdn.net/luoleicn/article/details/6527049）

解方程问题：

牛顿法最初用于求解方程根 f(x) = 0

首先得到一个初始解 x0，

一阶展开：f(x) ≈ f(x0)+(x－x0)f'(x0)

令 f(x0)+(x－x0)f'(x0) = 0

求解得到x，相比于x0，f(x)<f(x0)  (具体证明可以查看数值分析方面的书)

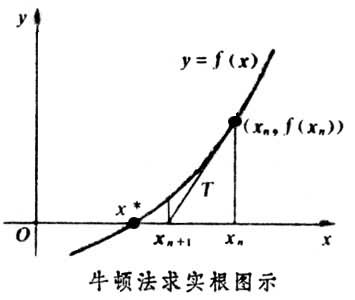
最优化问题中，牛顿法首先则是将问题转化为求 f‘(x) = 0 这个方程的根。

首先得到一个初始解 x0，

一阶展开：f ’(x) ≈ f ‘(x0)+(x－x0)f '’(x0)

令 f ‘(x0)+(x－x0)f '’(x0) = 0

求解得到x，相比于x0，f ‘(x)<f ’(x0)

也可以用上面借鉴的博文（也是wiki）中所说的那种方法，把 delta x 作为一个变量，让 f（x）对其偏导为0 什么的， 反正我记不住。

最小化f（x）之高维情况：

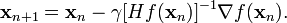
梯度 代替了低维情况中的一阶导

Hessian矩阵代替了二阶导

求逆 代替了除法

wiki上的一个图，可以看到 二者区别，

梯度下降法（绿色）总是沿着当前点最快下降的方向（几乎垂直于等高线），相当于贪心算法。

牛顿法利用了曲面本身的信息，能够更直接，更快的收敛。

A comparison of gradient descent(green) and Newton's method (red) for minimizing a function (with small step sizes). Newton's method uses curvature information to take a more direct route.

高斯牛顿法：

高斯牛顿法实际上是牛顿法的在求解非线性最小二乘问题时的一个特例。

目标函数：

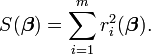
该函数是趋于0的，所以直接使用高维的牛顿法来求解。

迭代公式：

和牛顿法中的最优化问题高维迭代公式一样

目标函数可以简写：

,

梯度向量在方向上的分量：

                  （1）

Hessian 矩阵的元素则直接在梯度向量的基础上求导：

高斯牛顿法的一个小技巧是，将二次偏导省略，于是：

（2）

将(1)(2)改写成 矩阵相乘形式：

其中 Jr 是雅克比矩阵,r是 ri 组成的列向量。

代入牛顿法高维迭代方程的基本形式，得到高斯牛顿法迭代方程：

即

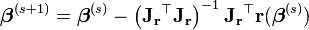， （wiki上的公式，我觉得分母写错了）

具体推导也可以看wiki

http://en.wikipedia.org/wiki/Gauss%E2%80%93Newton_algorithm#Derivation_from_Newton.27s_method

m ≥ n 是必要的，因为不然的话，J_r^TJ_{r肯定是不可逆的（利用rank(A'A) = rank(A)）}

若m=n：

拟合问题中：

由于Jf = -Jr

故用 Jf而不是Jr来表示迭代公式：

normal equations（法方程）：

delta实际是一个法方程，法方程是可以由方程推过来的，那么这个过程有什么意义呢？

其实高斯牛顿法可以利用一阶泰勒公式直接推导（直接当成解方程问题，而不是最优化问题，绕过求解H的过程）：

迭代之后的值：

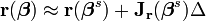
目标近似变成：

,

求解 delta 的过程实际就是法方程的推导过程。

之所以能够直接当做解方程问题，是因为目标函数的最优值要趋于0.

高斯牛顿法只能用于最小化平方和问题，但是优点是，不需要计算二阶导数。

Levenberg-Marquardt方法：

高斯-牛顿法中为了避免发散，有两种解决方法

1.调整下降步伐：. 

2.调整下降方向：

时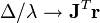：（这里好像wiki又错了），即方向和梯度方向一样，变成了梯度下降法。

相反，如果λ为0，就变成了高斯牛顿法。

Levenberg-Marquardt方法的好处在于可以调节:

如果下降太快，使用较小的λ，使之更接近高斯牛顿法

如果下降太慢，使用较大的λ，使之更接近梯度下降法

If reduction of S is rapid, a smaller value can be used, bringing the algorithm closer to the Gauss–Newton algorithm, whereas if an iteration gives insufficient reduction in the residual, λ can be increased, giving a step closer to the gradient descent direction.