求全排列Permutation

是在教材（《计算机算法设计与分析（第4版）》王晓东 编著）上看见的关于求全排列的算法；

我们可以看一下书上怎么写的：

#include<bits/stdc++.h>
using namespace std;
template<class Type>
void Perm(Type num[],int l,int r)
{
    if(l==r)
    {
        for(int i=;i<=r;i++) cout<<num[i]<<" ";
        cout<<endl;
    }
    else
    {
        for(int i=l;i<=r;i++)
        {
            swap(num[l],num[i]);
            Perm(num,l+,r);
            swap(num[l],num[i]);
        }
    }
}
int main()
{
    int num[]={,,,,,,};

    Perm(num,,);
    cout<<endl;

    Perm(num,,);
    cout<<endl;
}

看一下运行结果：

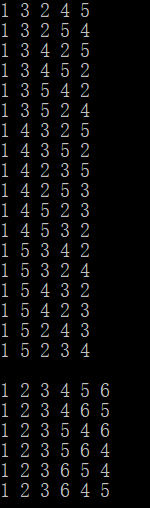
显然，这个函数在功能实现上……存在一定的问题（虽然思路上没问题），所以……

我自己重新写了一个，也许以后可能用的到呢：

#include<bits/stdc++.h>
using namespace std;
void Perm(int num[],int st,int ed,int l,int r)//st,ed表示选取的范围; l,r表示进行全排列的范围
{
    if(l==r)
    {
        for(int i=st;i<=ed;i++) cout<<num[i]<<" ";
        cout<<endl;
        return;
    }

    for(int i=l;i<=r;i++)
    {
        swap(num[l],num[i]);
        Perm(num,st,ed,l+,r);
        swap(num[l],num[i]);
    }
}
int main()
{
    int num[]={,,,,,,};

    Perm(num,,,,);
    cout<<endl;

    Perm(num,,,,);
    cout<<endl;
}