特征向量-Eigenvalues_and_eigenvectors#Graphs 线性变换

总结：

1、线性变换运算封闭，加法和乘法

2、特征向量经过线性变换后方向不变

https://en.wikipedia.org/wiki/Linear_map

Examples of linear transformation matrices

In two-dimensional space R² linear maps are described by 2 × 2 real matrices. These are some examples:

• rotation
  • by 90 degrees counterclockwise:

    

  • by an angle θ counterclockwise:

    

• reflection
  • about the x axis:

    

  • about the y axis:

    

• scaling by 2 in all directions:

  

• horizontal shear mapping:

  

• squeeze mapping:

  

• projection onto the y axis:

  

In mathematics, a linear map (also called a linear mapping, linear transformation or, in some contexts, linear function) is a mapping V → W between two modules (including vector spaces) that preserves (in the sense defined below) the operations of addition and scalar multiplication.

An important special case is when V = W, in which case the map is called a linear operator,^[1] or an endomorphism of V. Sometimes the term linear function has the same meaning as linear map, while in analytic geometry it does not.

A linear map always maps linear subspaces onto linear subspaces (possibly of a lower dimension);^[2] for instance it maps a plane through the origin to a plane, straight line or point. Linear maps can often be represented as matrices, and simple examples include rotation and reflection linear transformations.

In the language of abstract algebra, a linear map is a module homomorphism. In the language of category theory it is a morphism in the category of modules over a given ring.

Definition and first consequences

Let  and   be vector spaces over the same field  A function  is said to be a linear map if for any two vectors  and any scalar  the following two conditions are satisfied:

	additivity / operation of addition
	homogeneity of degree 1 / operation of scalar multiplication

Thus, a linear map is said to be operation preserving. In other words, it does not matter whether you apply the linear map before or after the operations of addition and scalar multiplication.

This is equivalent to requiring the same for any linear combination of vectors, i.e. that for any vectors  and scalars   the following equality holds:^[3][4]

Denoting the zero elements of the vector spaces  and   by   and   respectively, it follows that  Let  and  in the equation for homogeneity of degree 1:

 

Occasionally,   and   can be considered to be vector spaces over different fields. It is then necessary to specify which of these ground fields is being used in the definition of "linear". If  and  are considered as spaces over the field  as above, we talk about -linear maps. For example, the conjugation of complex numbers is an -linear map  , but it is not  -linear.

A linear map  with  viewed as a vector space over itself is called a linear functional.^[5]

These statements generalize to any left-module  over a ring  without modification, and to any right-module upon reversing of the scalar multiplication.

https://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors#Graphs

                    A               {\displaystyle A}   ，它的特征向量（eigenvector，也译固有向量或本征向量）                     v               {\displaystyle v}   经过这个线性变换^[1]之后，得到的新向量仍然与原来的                     v               {\displaystyle v}   保持在同一条直线上，但其长度或方向也许会改变。即

                    A               {\displaystyle A}   ，它的特征向量（eigenvector，也译固有向量或本征向量）                     v               {\displaystyle v}   经过这个线性变换^[1]之后，得到的新向量仍然与原来的                     v               {\displaystyle v}   保持在同一条直线上，但其长度或方向也许会改变。即

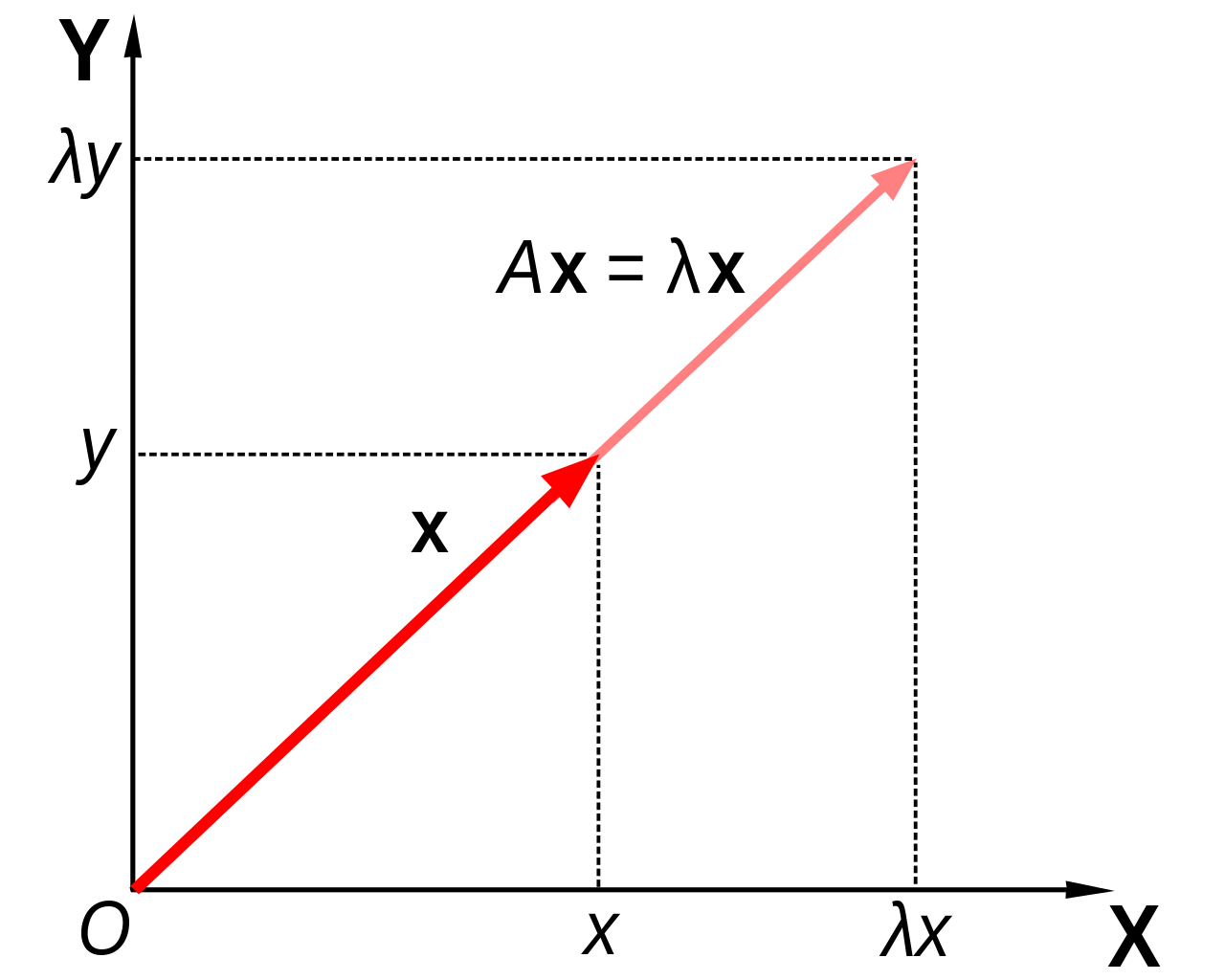
In linear algebra, an eigenvector or characteristic vector of a linear transformation is a non-zero vector that does not change its direction when that linear transformation is applied to it. More formally, if T is a linear transformation from a vector space V over a field F into itself and v is a vector in V that is not the zero vector, then v is an eigenvector of T if T(v) is a scalar multiple of v. This condition can be written as the equation

                    T         (                   v                 )         =         λ                   v                 ,               {\displaystyle T(\mathbf {v} )=\lambda \mathbf {v} ,}  

where λ is a scalar in the field F, known as the eigenvalue, characteristic value, or characteristic root associated with the eigenvector v.

If the vector space V is finite-dimensional, then the linear transformation T can be represented as a square matrix A, and the vector v by a column vector, rendering the above mapping as a matrix multiplication on the left hand side and a scaling of the column vector on the right hand side in the equation

                    A                   v                 =         λ                   v                 .               {\displaystyle A\mathbf {v} =\lambda \mathbf {v} .}  

There is a correspondence between n by n square matrices and linear transformations from an n-dimensional vector space to itself. For this reason, it is equivalent to define eigenvalues and eigenvectors using either the language of matrices or the language of linear transformations.^[1][2]

Geometrically an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction that is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed.^[3]

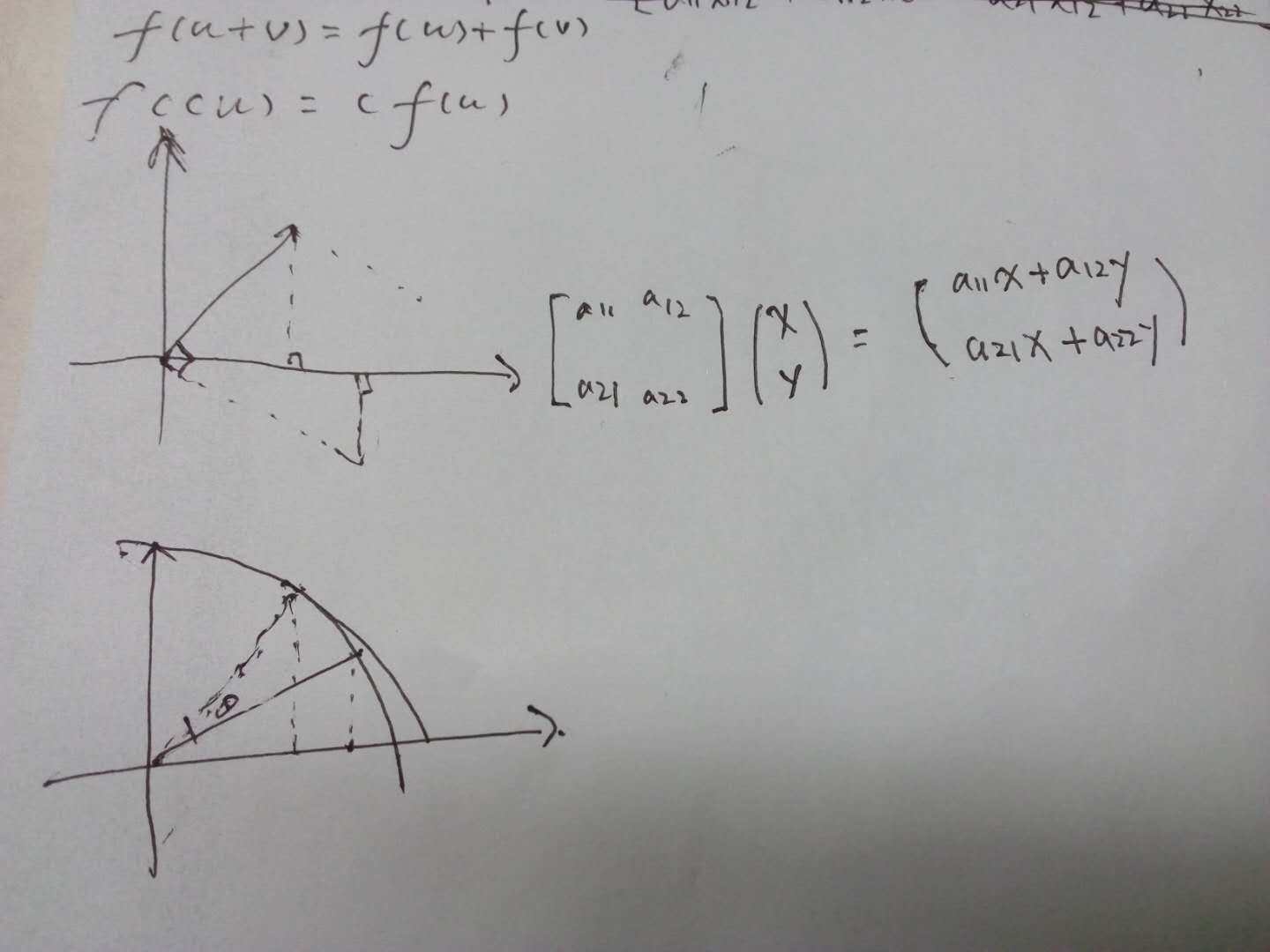
math.mit.edu/~gs/linearalgebra/ila0601.pdf

A100 was found by using the eigenvalues of A, not by multiplying 100 matrices.

                    A         v         =         λ         v               {\displaystyle Av=\lambda v}   ，

λ               {\displaystyle \lambda }   为标量，即特征向量的长度在该线性变换下缩放的比例，称                     λ               {\displaystyle \lambda }   为其特征值（本征值）。如果特征值为正，则表示                     v               {\displaystyle v}   在经过线性变换的作用后方向也不变；如果特征值为负，说明方向会反转；如果特征值为0，则是表示缩回零点。但无论怎样，仍在同一条直线上。

                    A         v         =         λ         v               {\displaystyle Av=\lambda v}   ，

λ               {\displaystyle \lambda }   为标量，即特征向量的长度在该线性变换下缩放的比例，称                     λ               {\displaystyle \lambda }   为其特征值（本征值）。如果特征值为正，则表示                     v               {\displaystyle v}   在经过线性变换的作用后方向也不变；如果特征值为负，说明方向会反转；如果特征值为0，则是表示缩回零点。但无论怎样，仍在同一条直线上。