【BZOJ4869】相逢是问候 [线段树][欧拉定理]

相逢是问候

Time Limit: 40 Sec  Memory Limit: 512 MB
[Submit][Status][Discuss]

Description

　　Informatikverbindetdichundmich.

　　信息将你我连结。B君希望以维护一个长度为n的数组，这个数组的下标为从1到n的正整数。一共有m个操作，可以

　　分为两种：0 l r表示将第l个到第r个数（al,al+1,...,ar）中的每一个数ai替换为c^ai，即c的ai次方，其中c是

　　输入的一个常数，也就是执行赋值ai=c^ai1 l r求第l个到第r个数的和，也就是输出：sigma(ai),l<=i<=rai因为

　　这个结果可能会很大，所以你只需要输出结果mod p的值即可。

Input

　　第一行有三个整数n,m,p,c，所有整数含义见问题描述。

　　接下来一行n个整数，表示a数组的初始值。

　　接下来m行，每行三个整数，其中第一个整数表示了操作的类型。

　　如果是0的话，表示这是一个修改操作，操作的参数为l,r。

　　如果是1的话，表示这是一个询问操作，操作的参数为l,r。

Output

　　对于每个询问操作，输出一行，包括一个整数表示答案mod p的值。

Sample Input

　　4 4 7 2
　　1 2 3 4
　　0 1 4
　　1 2 4
　　0 1 4
　　1 1 3

Sample Output

　　0
　　3

HINT

　　1 ≤ n ≤ 50000, 1 ≤ m ≤ 50000, 1 ≤ p ≤ 100000000, 0 < c <p, 0 ≤ ai < p

Solution

　　首先，我们运用欧拉定理：

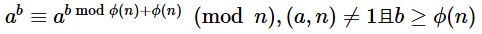
　　然后还有一个定理：一个数在执行log次操作后，值不会改变。

　　于是乎，我们可以运用线段树，暴力修改每一个值，如果值都不变了则不修改。

　　然后我们再考虑一下，怎么修改这个值：
　　已知a(原值)和times(修改次数)，我们考虑每一次%什么，
　　　　考虑每一次b的模数。
　　　　首先如果b%phi(p)，意味着a^b在%p下同余。
　　　　如果这一次b%phi(phi(p))，意味着a^b在phi(p)下同余，
　　　　同时也意味着下一次在%phi(p)意义下。
　　　　我们要让答案最后是在%p意义下的，那么显然每次b%phi[times-1]。
　　再带上快速幂，那么这样效率就是O(nlog^3(n))的。

Code

#include<iostream>
#include<string>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
using namespace std;
typedef long long s64;

const int ONE = ;
const int INF = ;

int n,m,p,C;
int opt,x,y;
int a[ONE],phi[ONE],p_num;
int MOD;
int res;

struct power
{
        int value;
        int cnt;
}Node[ONE];

int get()
{
        int res=,Q=;char c;
        while( (c=getchar())< || c> )
        if(c=='-')Q=-;
        res=c-;
        while( (c=getchar())>= && c<= )
        res=res*+c-;
        return res*Q;
}

int Getphi(int n)
{
        int res = n;
        for(int i=; i*i<=n; i++)
        if(n % i == )
        {
            res = res/i*(i-);
            while(n % i == ) n /= i;
        }
        if(n != ) res = res/n*(n-);
        return res;
}

int Quickpow(int a,int b,int MOD)
{
        int res = ;
        while(b)
        {
            if(b & ) res = (s64)res * a % MOD;
            a = (s64)a * a % MOD;
            b >>= ;
        }
        return res;
}

void Build(int i,int l,int r)
{
        if(l == r)
        {
            Node[i].value = a[l] % MOD;
            return;
        }
        int mid = l+r>>;
        Build(i<<, l, mid);
        Build(i<<|, mid + , r);
        Node[i].value = (Node[i<<].value + Node[i<<|].value) % MOD;
}

int Calc(int a, int times)
{
        for(int i=times; i>=; i--)
        {
            if(a >= phi[i]) a = a%phi[i] + phi[i];
            a = Quickpow(C, a, phi[i-]);
            if(!a) a = phi[i-];
        }
        return a;
}

void Update(int i,int l,int r,int L,int R)
{
        if(Node[i].cnt >= p_num) return;
        if(l == r)
        {
            Node[i].value = Calc(a[l], ++Node[i].cnt);
            return;
        }

        int mid = l+r>>;
        if(L <= mid) Update(i<<, l, mid, L, R);
        if(mid+ <= R) Update(i<<|, mid+, r, L, R);

        Node[i].value = (Node[i<<].value + Node[i<<|].value) % MOD;
        Node[i].cnt = min(Node[i<<].cnt, Node[i<<|].cnt);
}

void Query(int i,int l,int r,int L,int R)
{
        if(L<=l && r<=R)
        {
            res = (res + Node[i].value) % MOD;
            return;
        }

        int mid = l+r>>;
        if(L <= mid) Query(i<<, l, mid, L, R);
        if(mid+ <= R) Query(i<<|, mid+, r, L, R);
}

int main()
{
        n = get();    m = get();    p = get();    C = get();
        for(int i=; i<=n; i++) a[i] = get();

        MOD = phi[] = p;
        while(p!=) phi[++p_num] = p = Getphi(p);
        phi[++p_num] = ;
        Build(, , n);

        while(m--)
        {
            opt = get();
            x = get();    y = get();
            if(!opt) Update(, , n, x, y);
            else
            {
                res = ;
                Query(, , n, x, y);
                printf("%d\n", res);
            }
        }
}