LCA【Tarjan】

首先，我们先来了解LCA。

LCA 是树上两个点最近的公共祖先。

比如说，在如图的树中，3与4的公共祖先有“2”，“1”，但最近的祖先是“2”。

显然，暴力可以做O(n)，但是我们希望更快。

现在，有两种方法：

　　1）在线操作，但这需要“倍增”，再此不讨论。

　　2）离线操作，使用Tarjan与并查集。

先给出操作方法：

DFS (u)
   for i in u.son
      DFS(i)
      UNION(u,i)
   for i in u.e # e 表示 e 与访问所有和u有询问关系的i
      if i.vis
         (u,i).LCA = find(i)

可以发现，操作是在深搜中进行的。下面开始模拟。

初始值：

;
;
;
;
;
;

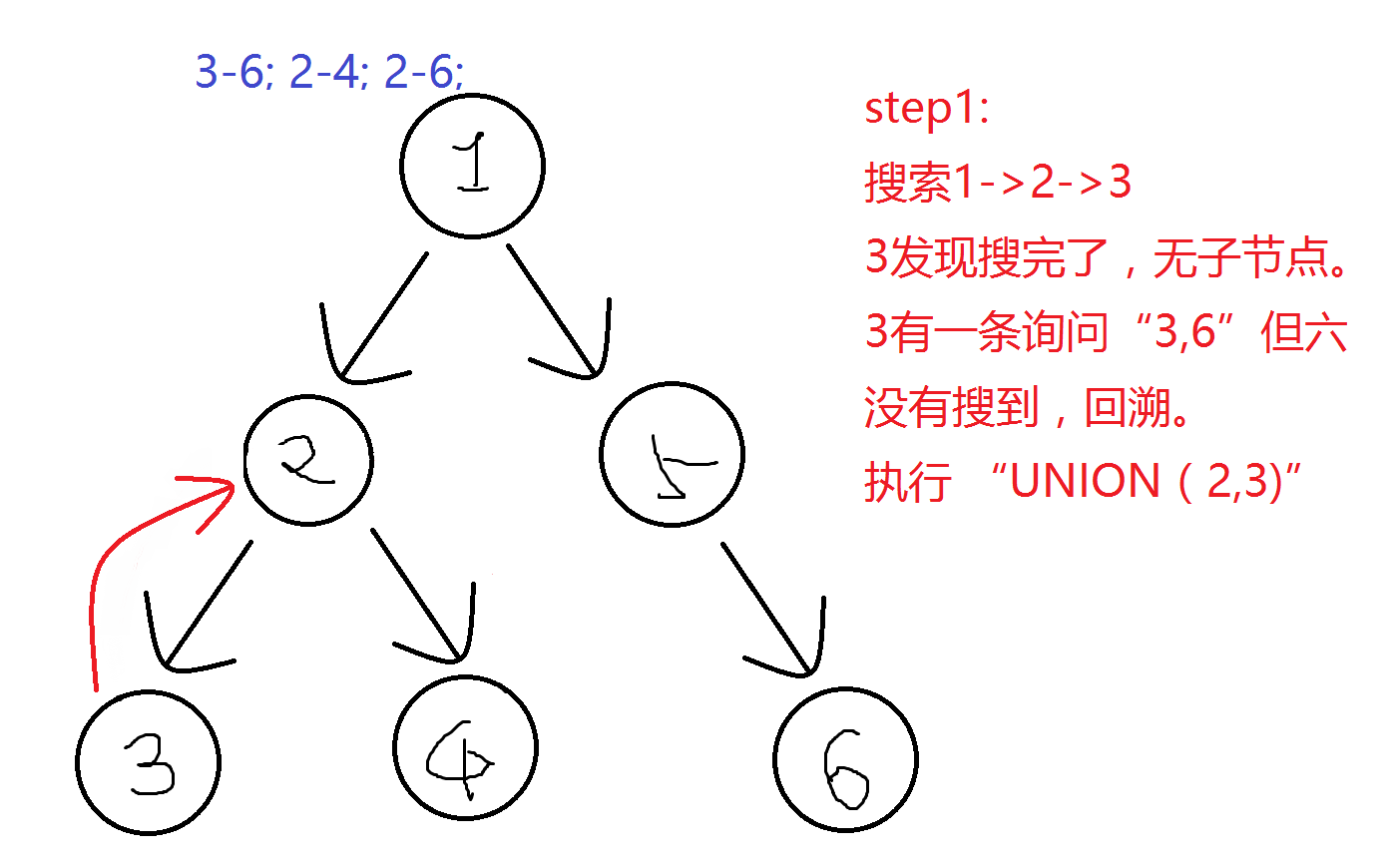
第一次操作后：

;
;
;
;
;
;

第二次操作后：

;
;
;
; 
;
;

第三次操作后：

;
;
;
;
;
;

另附代码：

#include <iostream>  
#include <stdio.h>  
#include <algorithm>  
#include <string.h>  
using namespace std;  
  
;
;   
int f[maxn];
int find(int x)  
{  
)  
        return x;  
    return f[x]=find(f[x]);  
}  
void unite(int u,int v)  
{  
    int x=find(u);  
    int y=find(v);  
    if(x!=y)  
        f[x]=y;  
}  
  
bool vis[maxn];
int ancestor[maxn];
struct Edge  
{  
    int to,next;  
];  
int head[maxn],tot;  
void addedge(int u,int v)
{  
    edge[tot].to=v;  
    edge[tot].next=head[u];  
    head[u]=tot++;  
}  
  
struct Query  
{  
    int q,next;  
    int index; 
];  
];
int h[maxn],tt;  
int Q;
  
void addquery(int u,int v,int index)
{  
    query[tt].q=v;  
    query[tt].next=h[u];  
    query[tt].index=index;  
    h[u]=tt++;  
    query[tt].q=u;
    query[tt].next=h[v];  
    query[tt].index=index;  
    h[v]=tt++;  
}  
  
void init()  
{  
;  
,sizeof(head));  
;  
,sizeof(h));  
,sizeof(vis));  
,sizeof(f));  
,sizeof(ancestor));  
}  
  
void LCA(int u)  
{  
    ancestor[u]=u;  
    vis[u]=true;  
;i=edge[i].next) 
    {  
        int v=edge[i].to;  
        if(vis[v])  
            continue;  
        LCA(v);  
        unite(u,v);  
        ancestor[find(u)]=u;
    }  
;i=query[i].next)
    {  
        int v=query[i].q;  
        if(vis[v])  
            ans[query[i].index]=ancestor[find(v)];  
    }  
}  
bool flag[maxn];
  
int t;  
int n,u,v;  
  
int main()  
{  
    cin >> n;  
    init();  
,sizeof(flag));  
;i<n;i++)  
    {  
        cin >> u >> v; 
        flag[v]=true; 
        addedge(u,v);  
        addedge(v,u);  
    }  
    cin >> Q;
;i<Q;i++)  
    {  
        scanf("%d%d",&u,&v);  
        addquery(u,v,i);  
    }  
    int root;  
    cin >> root;
    LCA(root);  
;i<Q;i++)  
        printf("%d\n",ans[i]);  
;  
}