P1058立体图

一道大模拟

思路：

首先是打表找规律时间

仔细思考（暴力手算）后推出这么一个数组：

//宽的增加量
int dm[]={,,,};//1竖着摞，2横着摞，3前后摞
//长的增加量
int dn[]={,,,};//1竖着摞，2横着摞，3前后摞 

这是什么意思呢？在初始的情况下，一个正方体的长是7个字符（对应了二维图的宽，就是y），高是6个字符（对应了二维图的长，就是x）

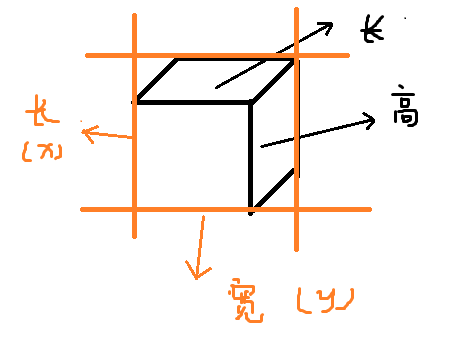如图，橙色表示二维图的参数，黑色表示三维正方体的参数

我们用1表示竖着摞，2表示横着摞，3表示前后摞

我们发现

• 每竖着摞一个正方体，二维图的宽是不会变的，但是长会在6的基础上+3
• 每横着摞一个正方体，二维图的宽在7的基础上增加4，长不变
• 每前后摞一个正方体，二维图的长和宽都在原来的基础上增加2

我们既然要输出最后的图，显然要先求出他的长和宽

宽是比较好求的，因为宽只与横着摞和前后摞有关，而这两个方式都可以直接又输入的n和m得出。设mm为输出图的宽，则：

　　mm=7+(n-1)*dm[3]+(m-1)*dm[2];

而长就不一样了，长不但与前后摞有关，还与上下摞有关，因为我没有ybr神仙那么强，所以我决定枚举。

    for(int i=;i<=n;i++)
    {
        for(int j=;j<=m;j++)
        {
            nn=max(nn,atlas[i][j]*dn[]+dn[]*(n-i+)+);
            //枚举每一个点的长，取最大值
        }
    }

于是我们就求出了长和宽，接下来考虑处理图。可以用一个点来代表整张图，这里我选择左下角的点，可以根据当前的位置（给的矩阵的某个位置）推出左下角的点，然后进行覆盖就好了。由于是按照从后向前，从左到右的顺序进行处理的，所以后来的会把先来的覆盖上，就处理了透视的问题

完整代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n,m;

char s1[][]=
{
    "..+---+",
    "./   /|",
    "+---+ |",
    "|   | +",
    "|   |/.",
    "+---+.."
};
//宽的增加量
int dm[]={,,,};//1竖着摞，2横着摞，3前后摞
//长的增加量
int dn[]={,,,};//1竖着摞，2横着摞，3前后摞 

char s[][];

int atlas[][];

int mm,nn; 

inline void zhetizhenduliu(int i,int j,int x,int y)
{
    int a,b;
    while(atlas[i][j]--)
    {
        for(a=;a<;a++)
        for(b=;b<;b++)
            if(s1[-a-][b]!='.')
                s[x-a][y+b]=s1[-a-][b];
        x-=;
    }

}

int main()
{
    //freopen("drawing.in","r",stdin);
    //freopen("drawing.out","w",stdout);
    n=read(),m=read();

    for(int i=;i<=;i++)
    {
        for(int j=;j<=;j++)
        {
            s[i][j]='.';
        }
    }

    for(int i=;i<=n;i++)
    {
        for(int j=;j<=m;j++)
        {
            atlas[i][j]=read();
        }
    }

    if(m==&&n==&&atlas[][]==)
    {
        printf("..+---+\n./   /|\n+---+ |\n|   | +\n|   |/.\n+---+..\n");
        return ;
    }

    mm=+(n-)*dm[]+(m-)*dm[];//求出输出的宽
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=m;j++)
        {
            nn=max(nn,atlas[i][j]*dn[]+dn[]*(n-i+)+);
            //枚举每一个点的长，取最大值
        }
    }

    for(int i=;i<=n;i++)
    {
        for(int j=,x,y;j<=m;j++)
        {
            x=nn-dn[]*(n-i);//考虑倒着搞，i前面的会产生2*(n-i)的影响
            y=dm[]*(n-i)+dm[]*(j-)+;
            zhetizhenduliu(i,j,x,y);
        }
    }
    for(int i=;i<=nn;i++)
    {
        for(int j=;j<=mm;j++)
        {
            printf("%c",s[i][j]);
        }
        puts("");
    }

}

PS：由于我太蒟了，考试的时候想到了做法但是覆盖的地方写炸，所以后来借鉴了题解（竟然和我思路差不多）