【NOI2019模拟2019.6.29】组合数（Lucas定理、数位dp）

Description：

---

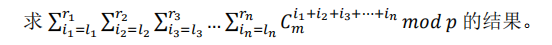
p<=10且p是质数，n<=7,l,r<=1e18

题解：

---

Lucas定理：

\(C_{n}^m=C_{n~mod~p}^{m~mod~p}*C_{n/p}^{m/p}\)

若把\(n,m\)在p进制下分解，那么就是\(\prod C_{n[i]}^{m[i]}\)。

对于\(∈[l,r]\)的限制先容斥为\(<=r\)。

考虑从低位到高位的数位dp，设\(f[i][S][j]\)表示做了前i位，S[i]第i个数选的数是<=还是>，进了j位，的系数和。

转移的话可以枚举每个数这一位选了什么，当然就是枚举<=或者>，当然这样还是很慢。

不妨再用一个dp来转移，设\(g[i][S][j]\)表示考虑了前i个数，现在的状压态是S，这一位的和是j，初值是\(g[0][S][j]=f[i][S][j]\)。

那么总时间复杂度大概是\(O(2^n*log_p^m*2^n*(pn)^2)\)

反正跑得过。

Code：

---

#include<bits/stdc++.h>
#define fo(i, x, y) for(int i = x, B = y; i <= B; i ++)
#define ff(i, x, y) for(int i = x, B = y; i <  B; i ++)
#define fd(i, x, y) for(int i = x, B = y; i >= B; i --)
#define ll long long
#define pp printf
#define hh pp("\n")
using namespace std;

int jx[11][11];
int n, p;
ll m, l[101], r[11], a[11];
int b[101], b0, c[11][101], c0[11];
int a2[10];
int ans;
int f[2][1 << 7][8], o;
int g[2][1 << 7][60], o2;

#define mem(a) memset(a, 0, sizeof a)
void dp(int xs) {
	mem(c);
	fo(i, 1, n) {
		ll v = a[i];
		c0[i] = 0;
		for(; v > 0; v /= p) c[i][++ c0[i]] = v % p;
	}
	mem(f); f[o][0][0] = 1;
	fo(i, 1, b0) {
		mem(f[!o]);
		mem(g);
		ff(j, 0, a2[n]) fo(k, 0, n - 1) g[o2][j][k] = f[o][j][k];
		fo(j, 1, n) {
			mem(g[!o2]);
			ff(s, 0, a2[n]) fo(k, 0, 48) if(g[o2][s][k]) {
				g[o2][s][k] %= p;
				int s2 = s & (a2[n] - 1 - a2[j - 1]);
				int ns = s2;
				int l = 0, r = c[j][i] - 1;
				fo(u, l, r) g[!o2][ns][k + u] += g[o2][s][k];
				ns = s;
				l = r = c[j][i];
				g[!o2][ns][k + l] += g[o2][s][k];
				ns = s2 + a2[j - 1];
				l = c[j][i] + 1, r = p - 1;
				fo(u, l, r) g[!o2][ns][k + u] += g[o2][s][k];
			}
			o2 = !o2;
		}
		ff(s, 0, a2[n]) fo(k, 0, 48) {
			f[!o][s][k / p] += g[o2][s][k] * jx[b[i]][k % p];
		}
		ff(s, 0, a2[n]) fo(k, 0, p - 1) f[!o][s][k] %= p;
		o = !o;
	}
	ff(s, 0, a2[n]) {
		int ky = 1;
		fo(j, 1, n) if((s >> (j - 1) & 1) && c0[j] <= b0) { ky = 0; break;}
		if(ky) ans = (ans + f[o][s][0] * xs) % p;
	}
}

void dg(int x, int xs) {
	if(x > n) {
		dp(xs);
		return;
	}
	a[x] = l[x] - 1; dg(x + 1, -xs);
	a[x] = r[x]; dg(x + 1, xs);
}

int main() {
	freopen("combination.in", "r", stdin);
	freopen("combination.out", "w", stdout);
	fo(i, 0, 7) a2[i] = 1 << i;
	scanf("%d %lld %d", &n, &m, &p);
	fo(i, 0, 10) {
		jx[i][0] = 1;
		fo(j, 1, i) jx[i][j] = (jx[i - 1][j - 1] + jx[i - 1][j]) % p;
	}
	fo(i, 1, n) scanf("%lld %lld", &l[i], &r[i]);
	for(; m; m /= p) b[++ b0] = m % p;
	dg(1, 1);
	ans = (ans % p + p) % p;
	pp("%d\n", ans);
}