计蒜客 18487.Divisions-大数的所有因子个数-Miller_Rabin+Pollard_rho-超快的(大数质因解+因子个数求解公式) (German Collegiate Programming Contest 2015 ACM-ICPC Asia Training League 暑假第一阶段第三场 F)

这一场两个和大数有关的题目，都用到了米勒拉宾算法，有点东西，备忘一下。

题目传送门

F. Divisions

传送门

这个题是求一个数的所有因子个数，但是数据比较大，1e18，所以是大数的题目，正常的求因数的或者求质因数的都过不了，因为这一场的K是米勒拉宾判大素数，先过的K题，所以这个题直接头铁用Miller_Rabin+Pollard_rho这两个东西+因子个数求解公式写过去了。

这两个算法的具体原理不清楚。从别人那里知道了一点。

Miller_Rabin算法的作用是判断一个数是否是个素数，算法速度很快，虽然是概率算法，有一定误判概率，不过可以多次运算大幅度减少误判，误判概率与运算次数t有关，为2^(-t)；当t够大时，误判的可能性就很小了。

Pollard_rho算法的作用是求一个数的因子，这个复杂度为O(sqrt(p)),p为这个数的因子。

参考来自别的的博客，传送门:算法集锦(特殊模板集)

因为Miller_Rabin+Pollard_rho这两个东西求出来的是一个数的所有质因数，所以最后要用因数个数求解公式来算出来结果。

关于因数个数求解公式:

对于任何一个自然数N，都可以分解质因子得到如下形式：

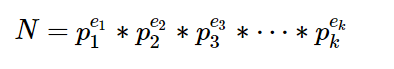
那么，N的因子的个数为：

如N=100，分解质因子变形为：100=2²∗5²，N的因子的个数为：f(N)=f(100)=(1+2)∗(1+2)=9。

即：1,2,4,5,10,20,25,50,100。

特判一下1就可以，找出来素因子之后，我是用map记了一下数然后用因子个数求解公式得到的结果。其他的没什么了。

代码:

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<iomanip>
 #include<stdio.h>
 #include<stdlib.h>
 #include<math.h>
 #include<cstdlib>
 #include<set>
 #include<map>
 #include<ctime>
 #include<stack>
 #include<queue>
 #include<vector>
 #include<set>
 using namespace std;
 typedef long long ll;
 const ll NUM=;//运算次数，Miller_Rabin算法为概率运算，误判率为2^(-NUM);
 ll t,f[];
 ll mul_mod(ll a,ll b,ll n)//求a*b%n，由于a和b太大，需要用进位乘法
 {
     a=a%n;
     b=b%n;
     ll s=;
     while(b)
     {
         if(b&)
             s=(s+a)%n;
         a=(a<<)%n;
         b=b>>;
     }
     return s;
 }
 ll pow_mod(ll a,ll b,ll n)//求a^b%n
 {
     a=a%n;
     ll s=;
     while(b)
     {
         if(b&)
             s=mul_mod(s,a,n);
         a=mul_mod(a,a,n);
         b=b>>;
     }
     return s;
 }
 bool check(ll a,ll n,ll r,ll s)
 {
     ll ans=pow_mod(a,r,n);
     ll p=ans;
     for(ll i=;i<=s;i++)
     {
         ans=mul_mod(ans,ans,n);
         if(ans==&&p!=&&p!=n-)
             return true;
         p=ans;
     }
     if(ans!=) return true;
     return false;
 }
 bool Miller_Rabin(ll n)//Miller_Rabin算法，判断n是否为素数
 {
     if(n<) return false;
     if(n==) return true;
     if(!(n&)) return false;
     ll r=n-,s=;
     while(!(r&)){r=r>>;s++;}
     for(ll i=;i<NUM;i++)
     {
         ll a=rand()%(n-)+;
         if(check(a,n,r,s))
             return false;
     }
     return true;
 }
 ll gcd(ll a,ll b)
 {
     return b==?a:gcd(b,a%b);
 }
 ll Pollard_rho(ll n,ll c)//Pollard_rho算法，找出n的因子
 {
     ll i=,j,k=,d,p;
     ll x=rand()%n;
     ll y=x;
     while(true)
     {
         i++;
         x=(mul_mod(x,x,n)+c)%n;
         if(y==x) return n;
         if(y>x) p=y-x;
         else p=x-y;
         d=gcd(p,n);
         if(d!=&&d!=n) return d;
         if(i==k)
         {
             y=x;
             k+=k;
         }
     }
 }
 void find(ll n)//找出n的所有因子
 {
     if(Miller_Rabin(n))
     {
         f[t++]=n;//保存所有因子
         return;
     }
     ll p=n;
     while(p>=n)p=Pollard_rho(p,rand()%(n-)+);//由于p必定为合数，所以通过多次求解必定能求得答案
     find(p);
     find(n/p);
 }
 int main()
 {
     srand(time(NULL));//随机数设定种子
     ll n;cin>>n;
     if(n==){cout<<""<<endl;return ;}
     t=;
     find(n);
     sort(f,f+t);
     map<ll,int>q;
     for(int i=;i<t;i++)
     {
         q[f[i]]++;
     }
     map<ll,int>::iterator it;
     ll ans=;
     for(it=q.begin();it!=q.end();it++)
     {
         int s=it->second;
         ans*=+s;
     }
     cout<<ans<<endl;
     return ;
 }