Tarjan缩点【p4819】[中山市选]杀人游戏

Description

一位冷血的杀手潜入Na-wiat，并假装成平民。警察希望能在\(N\)个人里面，查出谁是杀手。警察能够对每一个人进行查证，假如查证的对象是平民，他会告诉警察，他认识的人，谁是杀手，谁是平民。假如查证的对象是杀手，杀手将会把警察干掉。现在警察掌握了每一个人认识谁。每一个人都有可能是杀手，可看作他们是杀手的概率是相同的。

问：根据最优的情况，保证警察自身安全并知道谁是杀手的概率最大是多少？

Input

第一行有两个整数 \(N,M\)。 接下来有\(M\)行，每行两个整数 \(x,y\)，表示 \(x\) 认识 \(y\)（\(y\) 不一定认识 \(x\) ,例如President同志） 。

Output

仅包含一行一个实数，保留小数点后面 \(6\) 位，表示最大概率。

首先,如果一些人之间的关系存在环,那么我们可以只问其中的一个人就能知道这个环中的所有人的身份.可以降低我们的被害几率.

环?\(Tarjan\)缩点.

考虑到直接算安全的概率可能比较难算,所以我们考虑单步容斥.

安全概率=1-被杀概率

\(Tarjan\)缩点之后我们再次建图,会得到一个拓扑图.

这个拓扑图中,对于入度为\(0\)的一个点.显然,其会对被害几率有贡献.

因此我们记录图中入度为\(0\)的点的个数.

但是会存在一种情况,类似这样.

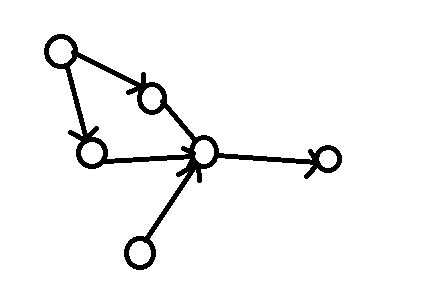
显然这个时候如果我们从左上角的点开始调查,发现没有杀手.

则杀手必定在下边的点中(这个点\(size\)必须为1,并且与其相连的点必须有其他入度).

确保自身安全的情况下,我们已经知道了杀手是谁.因此,这种点对答案并没有贡献.

且至多会有一个,

在代码中判断一下即可.

代码

#include<cstdio>
#include<cctype>
#include<iostream>
#define N 100008
#define R register
using namespace std;
inline void in(int &x)
{
	int f=1;x=0;char s=getchar();
	while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
	while(isdigit(s)){x=x*10+s-'0';s=getchar();}
	x*=f;
}
int n,m,head[N],tot,ttt,h[N],size[N],col;
struct cod{int u,v;}edge[N<<5],e[N<<2];
inline void add(int x,int y)
{
	edge[++tot].u=head[x];
	edge[tot].v=y;
	head[x]=tot;
}
inline void ado(int x,int y)
{
	e[++ttt].u=h[x];
	e[ttt].v=y;
	h[x]=ttt;
}
int dfn[N],low[N],top,idx,stk[N],ins[N],now,belong[N];
bool inq[N],flg;
void tarjan(int u)
{
	dfn[u]=low[u]=++idx;
	stk[++top]=u;inq[u]=true;
	for(R int i=head[u];i;i=edge[i].u)
	{
		if(!dfn[edge[i].v])
		{
			tarjan(edge[i].v);
			low[u]=min(low[u],low[edge[i].v]);
		}
		else if(inq[edge[i].v])
			low[u]=min(low[u],dfn[edge[i].v]);
	}
	if(low[u]==dfn[u])
	{
		int now=-1;col++;
		while(now!=u)
		{
			now=stk[top--];
			size[col]++;
			inq[now]=false;
			belong[now]=col;
		}
	}
}
inline bool pd(int x)
{
	for(R int i=h[x];i;i=e[i].u)
		if(ins[e[i].v]==1)return false;
	return true;
}
int ans;
int main()
{
	in(n),in(m);
	for(R int i=1,x,y;i<=m;i++)
	{
		in(x),in(y);
		add(x,y);
	}
	for(R int i=1;i<=n;i++)
		if(!dfn[i])tarjan(i);
	for(R int x=1;x<=n;x++)
		for(R int i=head[x];i;i=edge[i].u)
			if(belong[edge[i].v]!=belong[x])
				ins[belong[edge[i].v]]++,ado(belong[x],belong[edge[i].v]);
	for(R int x=1;x<=col;x++)
	{
		if(!flg and size[x]==1 and !ins[x] and pd(x))flg=true;
		if(!ins[x])ans++;
	}
	if(flg)ans--;
	printf("%.6f",1-(double)((double)ans/(double)n));
}