Codeforces 922.F Divisibility

F. Divisibility

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Imp is really pleased that you helped him. But it you solve the last problem, his gladness would raise even more.

Let's define 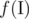 for some set of integers  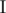as the number of pairs a, b in 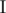, such that:

• a is strictly less than b;
• a divides b without a remainder.

You are to find such a set 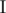, which is a subset of {1, 2, ..., n} (the set that contains all positive integers not greater than n), that .

Input

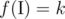The only line contains two integers n and k .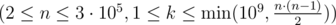

Output

If there is no answer, print "No".

Otherwise, in the first line print "Yes", in the second — an integer m that denotes the size of the set 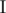 you have found, in the second line print m integers — the elements of the set 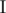, in any order.

If there are multiple answers, print any of them.

Examples

input

Copy

3 3

output

No

input

Copy

6 6

output

Yes
5
1 2 4 5 6 

input

Copy

8 3

output

Yes
4
2 4 5 8

Note

In the second sample, the valid pairs in the output set are (1, 2), (1, 4), (1, 5), (1, 6), (2, 4), (2, 6). Thus, .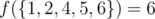

In the third example, the valid pairs in the output set are (2, 4), (4, 8), (2, 8). Thus, .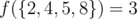

题目大意：在1~n中选任意个数组成一个集合I,定义f(I) = I中的每个数被I中的其它的多少个数整除的和.已知f(I) = k,求I.

分析：全程凭感觉做的一道题......

　　　令d(i)表示i被1~i-1这些数整除的数的个数,e(i) = Σd(j) (1 ≤ j ≤ i).首先需要猜出一个结论：当e(n) ≥ k时，是肯定有解的. 更近一步，当e(i) ≥ k时，肯定有解，那么就可以把＞i的数给丢掉.

　　　假设e(pos) ≥ k,k变成e(pos) - k,将pos / 2 + 1到pos的d全都加入优先队列中，每次弹出最大的d,如果k≥d,则k -= d,并丢掉这个d对应的i.这是基本做法，为什么只需要pos / 2 + 1到pos的数就可以了呢？

　　　如果考虑的数≤pos / 2,那么删掉这个数的贡献就不只是d,因为[pos / 2 + 1,pos]中有数是它的倍数,这个不好考虑.那为什么只考虑pos / 2 + 1到pos的数就一定最后能让k变成0呢？整除数m的数的个数是O(m ^ (1/3))的.而＞m/2并且＜m的质数的个数大约是个,一般后者的数量都比前者大，而质数的贡献是1，所以只删去质数就能满足要求，有极少数的数会出现后者比前者小，由于差的非常小，按照上述方法贪心地删就好了.

　　　如果不按照d来考虑贡献，可以考虑只删除1~pos的质数，对于质数i,它的贡献是[pos / i],删除当前质数不影响其他质数的贡献,其实和上面的贪心方法差不多.

　　　我曾经考虑过正向构造，每次考虑添加哪个数进去，但是贡献不好算,而且想不到什么好的策略. 这个方法就是把可能的数摆在你的面前，你要在里面删数,不仅要考虑能否满足要求，并且还要考虑贡献的计算问题. 挺考验数学直觉的.

#include <cstdio>
#include <queue>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

int n,k,sum[],d[],cur,leftt,vis[],ans;
priority_queue <pair<int,int> >q;

int main()
{
    scanf("%d%d",&n,&k);
    for (int i = ; i <= n; i++)
        for (int j = i * ; j <= n; j += i)
            d[j]++;
    for (int i = ; i <= n; i++)
    {
        sum[i] = sum[i - ] + d[i];
        if (sum[i] >= k)
        {
            leftt = sum[i] - k;
            cur = i;
            break;
        }
    }
    if (!cur)
        puts("No");
    else
    {
        puts("Yes");
        if (leftt == )
        {
            printf("%d\n",cur);
            for (int i = ; i <= cur; i++)
                printf("%d ",i);
        }
        else
        {
            for (int i = cur /  + ; i <= cur; i++)
                q.push(make_pair(d[i],i));
            while (leftt)
            {
                pair <int,int> temp = q.top();
                q.pop();
                if (leftt >= temp.first)
                {
                    leftt -= temp.first;
                    vis[temp.second] = ;
                }
            }
            for (int i = ; i <= cur; i++)
                if (!vis[i])
                    ans++;
            printf("%d\n",ans);
            for (int i = ; i <= cur; i++)
                if (!vis[i])
                    printf("%d ",i);
        }
    }

    return ;
}