二叉搜索树-php实现 插入删除查找等操作

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

　　以前只是知道又这么一种树但是没怎么去了解，这次查看了算法导论上介绍的思路, 用php写了个例子。

节点类

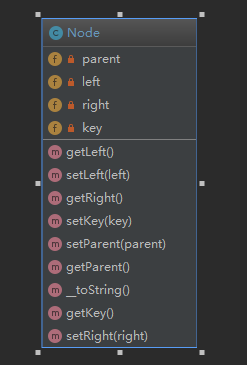
BST树类

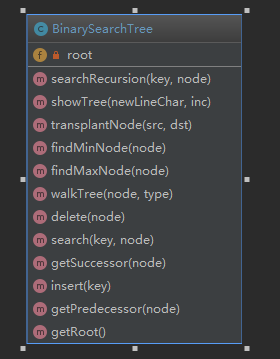
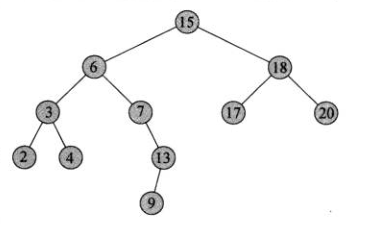
二叉搜索树样图

下面介绍下大致的操作

一  遍历

二叉搜索树可以通过简单的递归来遍历所有节点的关键词, 根据根,以及左右子树的输出顺序分为3种

(左根右) 中序遍历  [2 3 4 6 7 9 13 15 17 18 20]

(根左右) 先序遍历  [15 6 3 2 4 7 13 9 18 17 20]

(左右根) 后序遍历  [2 4 3 9 13 7 6 17 20 18 15]

中序遍历 示例

    /**
     * 遍历节点,获取key数组
     * @param Node $node 节点
     * @param int $type 遍历类型 0 中序 1 前序 2 后序
     * @return array
     * @author zxqc2018
     */
    public function walkTree(Node $node, int $type = 0)
    {
        $keyArr = [];
        $walkTreeFunc = function (?Node $node) use (&$keyArr, &$walkTreeFunc, $type){
            if (!is_null($node)) {
                if ($type === 1) {
                    $keyArr[] = $node->getKey();
                    $walkTreeFunc($node->getLeft());
                    $walkTreeFunc($node->getRight());
                }  else if ($type == 2) {
                    $walkTreeFunc($node->getLeft());
                    $walkTreeFunc($node->getRight());
                    $keyArr[] = $node->getKey();
                } else {
                    $walkTreeFunc($node->getLeft());
                    $keyArr[] = $node->getKey();
                    $walkTreeFunc($node->getRight());
                }
            }
        };

        $walkTreeFunc($node);

        return $keyArr;
    }

二 查找节点

非递归查找

    /**
     * 根据key, 查找节点
     * @param int $key
     * @param Node|null $node
     * @return Node|null
     * @author zxqc2018
     */
    public function search(int $key, Node $node = null)
    {
        if (is_null($node)) {
            $node = $this->getRoot();
        }

        while (!is_null($node) && $key != $node->getKey()) {
            if ($key < $node->getKey()) {
                $node = $node->getLeft();
            } else {
                $node = $node->getRight();
            }
        }

        return $node;
    }

递归查找

    /**
     * 根据key, 查找节点
     * @param int $key
     * @param Node|null $node
     * @return mixed
     * @author zxqc2018
     */
    public function searchRecursion(int $key, Node $node = null)
    {
        if (is_null($node)) {
            $node = $this->getRoot();
        }

        $recursionFunc = function ($key, Node $node) use (&$recursionFunc) {
            if (is_null($node) || $node->getKey() == $key) {
                return $node;
            }

            if ($key < $node->getKey()) {
                return $recursionFunc($key, $node->getLeft());
            } else {
                return $recursionFunc($key, $node->getRight());
            }
        };
        return $recursionFunc($key, $node);
    }

三 查找最大或小节点

最小节点

    /**
     * 查找最小节点
     * @param Node|null $node
     * @return Node|null
     * @author zxqc2018
     */
    public function findMinNode(Node $node)
    {
        if (!is_null($node)) {
            while (!is_null($node->getLeft())) {
                $node = $node->getLeft();
            }
        }
        return $node;
    }

最大节点

    /**
     * 查找最大节点
     * @param Node|null $node
     * @return Node|null
     * @author zxqc2018
     */
    public function findMaxNode(Node $node)
    {
        if (!is_null($node) && !is_null($node->getRight())) {
            $node = $this->findMaxNode($node->getRight());
        }
        return $node;
    }

四 后继和前驱

一颗二叉搜索树,按照中序遍历(从小到大)后的次序,  给定某个节点, 那么 后继 则是 此节点之后的那个节点, 前驱 则反之

查找后继有两种情况

1 节点的右孩子非空,   则后继是 右节点为根的子树种 关键字 最小的节点 。

2 节点的右孩子是空 并且有后继(树中的最大关键字的节点无后继)。那么 后继是  给点节点 最早有左孩子的底层祖先。

拿上面样图中 13 这个节点的 举例 。13的 第一个祖先 是 7 ,由于 13 是7的右孩子,所以肯定比 7 大,而 7的左孩子也肯定比 13 小 ,  以此类推, 到 6 的时候,是 祖先的 左孩子 , 说明 6 的祖先 肯定 比 13 , 也是祖先中比   13 大的 最小的节点。

后置

    /**
     * 获取节点的后继
     * @param Node $node
     * @return Node|null
     * @author zxqc2018
     */
    public function getSuccessor(Node $node)
    {
        //是否有右孩子
        if (!is_null($node->getRight())) {
            return $this->findMinNode($node->getRight());
        }

        $y = $node->getParent();

        //向上逐层判断是否为祖先的右孩子
        while (!is_null($y) && $node === $y->getRight()) {
            $node = $y;
            $y = $y->getParent();
        }

        return $y;
    }

前驱

    /**
     * 获取节点的前驱
     * @param Node $node
     * @return Node|null
     * @author zxqc2018
     */
    public function getPredecessor(Node $node)
    {
        //是否有左孩子
        if (!is_null($node->getLeft())) {
            return $this->findMaxNode($node->getLeft());
        }

        $y = $node->getParent();

        //向上逐层判断是否为祖先的左孩子
        while (!is_null($y) && $node === $y->getLeft()) {
            $node = $y;
            $y = $y->getParent();
        }

        return $y;
    }

五 插入

    /**
     * 插入节点key
     * @param int $key
     * @return Node
     * @author zxqc2018
     */
    public function insert(int $key)
    {
        $x = $this->getRoot();
        $y = null;
        $z = new Node($key);

        while (!is_null($x)) {
            $y = $x;
            if ($key < $x->getKey()) {
                $x = $x->getLeft();
            } else {
                $x = $x->getRight();
            }
        }

        //设置插入节点的父节点
        $z->setParent($y);

        //假如树还没根节点
        if (is_null($y)) {
            $this->root = $z;
        } else if ($key < $y->getKey()) {
            $y->setLeft($z);
        } else {
            $y->setRight($z);
        }

        return $z;
    }

六 删除

删除的情况比较复杂可以分为3种

假如 删除节点  为 z

1) z没有孩子

z的父节点用null 来替换 $z节点

2) z有一个孩子

假如z有一个右孩子,  z的右孩子 替换 z, 并且 z右孩子的父节点指向 z的父节点  ,如下图

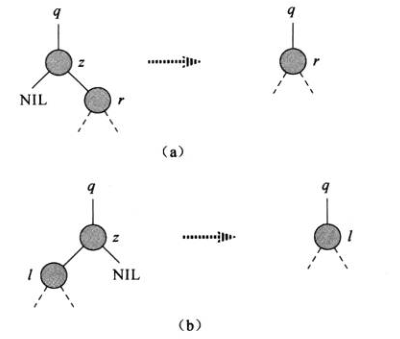
3) z有两个孩子

可以找到$z节点的后继或者前驱节点来替换$z, 达到删除,并且不破坏树结构的目的。 这里选后继来举例, 可以分成2种情况

假如 后继节点 为 y

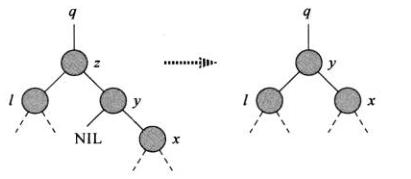
a) z的右孩子就是它的后继节点

y 替换 z 节点,  y的左孩子指向 z 的 左孩子,  z的 左孩子的 父节点指向 y,  y的父节点指向  z 节点的父节点

这里由个情况要说明就是 , z 的 后继节点 的左孩子肯定为null, 假如不是null 的话那么z 的后继就是y的左孩子了, 所以 z的后继 y 肯定是没有左孩子的

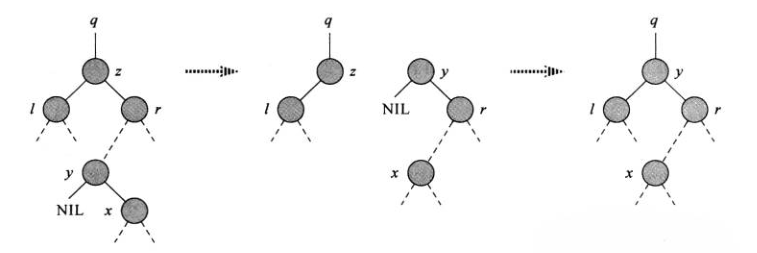
b) z的右孩子不是它的后继节点

这情况通过转换下就可以和上面情况一致了,所以只需转换下就OK了

y的右孩子替换 y, y 的右孩子 改成 z 的右孩子,  z 的右孩子的 父节点 由 z 改为 y,  这样转换后  就和上面的情况一致了

为什么可以这样转换?

y的右孩子替换 y,   这操作 等同于 删除y 节点 操作

y改为 z 的 右孩子的 父亲,  因为 y 是z 的后继 所以  y 肯定是 z 的右边 子树 中最小的,  所以   y 可以 作为  z 的 右孩子的父亲 , 没有破坏  树的结构

删除代码

    /**
     * 移动节点
     * @param Node $src 源节点
     * @param Node $dst 目标节点
     * @author zxqc2018
     */
    protected function transplantNode(?Node $src, Node $dst)
    {
        if (is_null($dst->getParent())) {
            $this->root = $src;
        }else if ($dst === $dst->getParent()->getLeft()) {
            $dst->getParent()->setLeft($src);
        } else {
            $dst->getParent()->setRight($src);
        }

        //源节点不空,则把源节点父节点指向目标节点的父节点
        if (!is_null($src)) {
            $src->setParent($dst->getParent());
        }
    }

    /**
     * 删除节点
     * @param Node $node
     * @author zxqc2018
     */
    public function delete(Node $node)
    {
         if (is_null($node->getLeft())) {
            $this->transplantNode($node->getRight(), $node);
        } else if (is_null($node->getRight())) {
            $this->transplantNode($node->getLeft(), $node);
        } else {
            $successorNode = $this->getSuccessor($node);
            //删除节点的右孩子不是后继节点,则做相应转换
            if ($node->getRight() !== $successorNode) {
                //后继节点的右孩子替换后继节点
                $this->transplantNode($successorNode->getRight(), $successorNode);
                //设置删除节点的右孩子为后继节点的右孩子
                $successorNode->setRight($node->getRight());
                //删除节点的右孩子的父节点改为后继节点
                $successorNode->getRight()->setParent($successorNode);
            }

            //后继节点替换删除节点
            $this->transplantNode($successorNode, $node);
            //设置删除节点的左孩子为后继节点的左孩子
            $successorNode->setLeft($node->getLeft());
            //删除节点的左孩子的父节点改为后继节点
            $successorNode->getLeft()->setParent($successorNode);
        }
    }

代码地址

https://github.com/zxqc/Share