算法训练 Pollution Solution（计算几何）

问题描述

　　作为水污染管理部门的一名雇员，你需要监控那些被有意无意倒入河流、湖泊和海洋的污染物。你的其中一项工作就是估计污染物对不同的水生态系统（珊瑚礁、产卵地等等）造成的影响。

　　你计算所使用的模型已经在图1中被说明。海岸线（图1中的水平直线）为x轴，污染源位于原点(0, 0)。污染的蔓延呈半圆形，多边形代表了被波及的生态系统。你需要计算出生态系统被污染的面积，也就是图中深蓝色部分。

输入格式

　　输入文件包含仅包含一组测试数据。
　　每组测试数据第一行为两个整数n (3 <= n <= 100), r (1 <= r <= 1000)，n表示了多边形的顶点个数，r表示了污染区域的半径；
　　接下来n行，每行包含两个整数xi (-1500 <= xi <= 1500), yi (0 <= yi <=1500)，表示每个顶点的坐标，以逆时针顺序给出；
　　数据保证多边形不自交或触及自身，没有顶点会位于圆弧上。

输出格式

　　输出多边形被圆心位于原点、半径为r的半圆覆盖的面积。
　　答案的绝对误差不得超过10^-3。

样例输入

6 10
-8 2
8 2
8 14
0 14
0 6
-8 14

样例输出

101.576437872

数据规模和约定

　　存在约30%的数据，n = 3，r <= 20；
　　存在另外约30%的数据，n <= 10，r <= 100，坐标范围不超过100；
　　存在另外约10%的数据，n <= 100，r <= 150，坐标范围不超过250；
　　存在另外约30%的数据，n <= 100，r <= 1000，数据存在梯度；
　　对于100%的数据，满足题目所示数据范围。

题解

#include<iostream>
#include<math.h>
#include<cstdio>
#include<algorithm>
#include<string>
#include<queue>
#include<cctype>
#include<cstring>
#include<map>
using namespace std;
const int N=1e2+5;
const int M=N/2;

int n,r;
int X[N],Y[N];

struct P{
    double x,y;
    double getlength(){
        return sqrt(x*x+y*y);
    }
    bool incircle(){
        return x*x+y*y<=r*r;
    }
    double cross(P &b){
        return x*b.y-y*b.x;
    }
};
double getArea(P &a,P &b){
    double degree=a.cross(b)/a.getlength()/b.getlength();
    if(degree<-1)degree=-1;
    if(degree>1)degree=1;
    degree=asin(degree);
    return r*r*degree/2;
}
double cal(P &a,P &b){
    bool in1 = a.incircle();
    bool in2 = b.incircle();
    if(in1&&in2){
        return a.cross(b)/2;
    }else if(in1!=in2){
        P l=a;
        P r=b;
        P mid;
        for(int i=0;i<40;i++){
            mid=P{(l.x+r.x)/2,(l.y+r.y)/2};
            if(mid.incircle()==in1){
                l=mid;
            }else{
                r=mid;
            }
        }
        if(in1){
            return a.cross(mid)/2+getArea(mid,b);
        }else{
            return getArea(a,mid)+mid.cross(b)/2;
        }
    }else{
        P l=a;
        P r=b;
        P mid;
        P midr;
        for(int i=0;i<40;i++){
            mid=P{(l.x+r.x)/2,(l.y+r.y)/2};
            midr=P{(l.x+r.x)/2+(r.x-l.x)*0.0001,(l.y+r.y)/2+(r.y-l.y)*0.0001};
            if(mid.getlength()<midr.getlength()){
                r=mid;
            }else{
                l=mid;
            }
        }
        if(mid.incircle()){
            return cal(a,mid)+cal(mid,b);
        }else{
            return getArea(a,b);
        }
    }
}

int main() {
    cin>>n>>r;
    for(int i=0;i<n;i++){
        cin>>X[i]>>Y[i];
    }
    X[n]=X[0];
    Y[n]=Y[0];
    double ans=0;
    for(int i=0;i<n;i++){
        P a=P{X[i],Y[i]};
        P b=P{X[i+1],Y[i+1]};
        ans+=cal(a,b);
    }
    printf("%lf\n",ans);

    return 0;
}

　　

看不懂系列》》》》

借助这道题补一下计算几何中的部分知识

1.容斥定理：要计算几个集合并集的大小，我们要先将所有单个集合的大小计算出来，然后减去所有两个集合相交的部分，再加回所有三个集合相交的部分，再减去所有四个集合相交的部分，依此类推，一直计算到所有集合相交的部分。

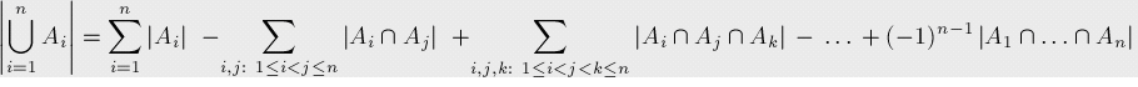
2.四色定理：四色问题的内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。”也就是说在不引起混淆的情况下一张地图只需四种颜色来标记就行。

3.点积：

点：A（x1，y1），B（x2，y2） 向量：向量AB=（ x2 - x1 , y2 - y1 ）= ( x , y );

向量的模 |AB| = sqrt ( x*x+y*y );

向量的点积： 结果为 x1*x2 + y1*y2。 点积的结果是一个数值。

点积的集合意义：我们以向量 a 向向量 b 做垂线，则 | a | * cos（a,b）为 a 在向量 b 上的投影，即点积是一个向量在另一个向量上的投影乘以另一个向量。且满足交换律

应用：可以根据集合意义求两向量的夹角， cos（a,b） =（ 向量a * 向量b ） / （| a | * | b |） = x1*x2 + y1*y2 / （| a | * | b |）

4.叉积：

向量的叉积： 结果为 x1*y2-x2*y1 叉积的结果也是一个向量，是垂直于向量a，b所形成的平面，如果看成三维坐标的话是在 z 轴上，上面结果是它的模。

方向判定：右手定则，（右手半握，大拇指垂直向上，四指右向量a握向b，大拇指的方向就是叉积的方向）

叉积的集合意义： 1：其结果是a和b为相邻边形成平行四边形的面积。 2：结果有正有负，有sin（a，b）可知和其夹角有关，夹角大于180°为负值。 3：叉积不满足交换律

应用： （1：通过结果的正负判断两矢量之间的顺逆时针关系 若 a x b > 0表示a在b的顺时针方向上 若 a x b < 0表示a在b的逆时针方向上 若 a x b == 0表示a在b共线，但不确定方向是否相同

（2：判断折线拐向，可转化为判断第三点在前两的形成直线的顺逆时针方向，然后判断拐向。

（3：判断一个点在一条直线的那一侧，同样上面的方法。

（4：判断点是否在线段上，可利用叉乘首先判断是否共线，然后在判断是否在其上。

（5：判断两条直线是否想交（跨立实验） 根据判断点在直线那一侧我们可以判断一个线段的上的两点分别在另一个线段的两侧，当然这是不够的，因为我们画图发现这样只能够让直线想交，而不是线段，所以我们还要对另一条线段也进行相同的判断就ok。

5.凸包：graham扫描法

6.皮克公式：（计算多边形的面积）

S = 1/2×( ( X1*Y2-X2*Y1 ) + … + ( Xk*Yk+1-Xk+1*Yk ) + ... + ( Xn*Y1-X1*Yn ) )

需要注意的是，如果一系列点按逆时针排列算出的是正面积，而如果是顺时针的话算出的则是一个负面积。