kosaraju算法

这个是求一个图有几个强联通分量的算法

先讲一下应该流程

首先输入一个图G，创建一个反向的图GT

图G

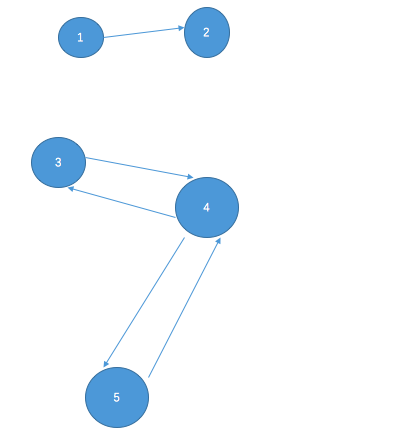
对图进行dfs遍历，纪录每个点结束搜索的时间p[i]

p[1]=2  p[2]=1  p[3]=5  p[4]=4  p[5]=3

接下来对GT进行dfs搜索

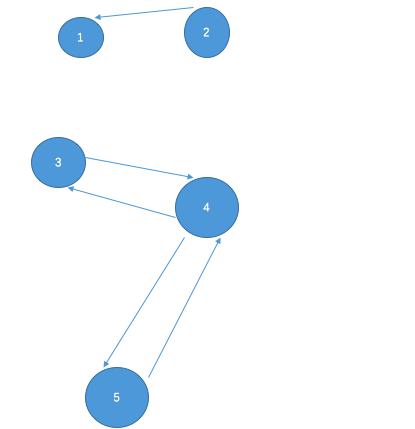
对图GT进行搜索的时候，先从之前纪录的时间最晚的点开始搜索

就是从点3开始搜索

若是3能在反向图中搜索到4意味着正向图中存在一条4->3的路   意思就是3和4互相抵达构成连通分量

因为是时间从晚到早  所以不存在说从中间的某个点开始的情况

意思就是不会出现下面的情况：

　　对GT进行搜索

　　先从2开始 搜索到1

　　1之后没有点  纪录12是一个连通分量

　　接下来345是一个连通分量

　　但其实12不是一个连通分量

所以我们从最晚的点开始搜索来避免这种情况

接下来介绍为什么从最晚的点开始搜索能避免这种情况

一个新图 只有1、2两个点

1点是在2点之后结束搜索的

那么有两种情况  第一种是 dfs(1)->dfs(2)->dfs(2)结束->dfs(1)结束

　　　　　　　　第二种   dfs(2)->dfs(2)结束  dfs(1)->dfs(1)结束

因为我们是从最后结束的点开始搜索

即对反向图从1开始搜索

那么假设反向图中1能搜索到2   那么说明原图的2能到达1

既然原图的2能够到达1   那么就不会出现dfs(2)->dfs(2)结束  dfs(1)->dfs(1)结束这种情况

否则为什么dfs(2)不进入dfs(1)呢

所以原图的1能够到达2

然后就是GT图   1能搜索到2   那么原图2能搜索到1   说明1和2连通

结论：按原图dfs结束时间对方向图进行搜索，搜索到的点都能够构成连通分量

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
const int maxn = ;
vector<int> G[maxn],G2[maxn];
int p[maxn];
bool q[maxn];
int n;
int cnt = ;
void dfs(int u);
void dfs2(int u);
int main()
{
    int i,j;
    char str[];
    scanf("%d",&n);
    for(i=;i<=n;++i)
    {
        scanf("%s",str+);
        for(j=;j<=n;++j)
        {
            if(str[j] == '')
            {
                G[i].push_back(j);
                G2[j].push_back(i);
            }
        }
    }
    memset(q, , sizeof(q));
    for(i=;i<=n;++i)
        dfs(i);
    int sum = ;
    memset(q, , sizeof(q));
    for(i=n;i>=;--i)
    {
        if(q[p[i]] == false)
        {
            sum ++ ; dfs2(p[i]);
        }
    }
    cout << sum << endl;
    return ;
}
void dfs(int u)
{
    q[u] = true;
    for(int i=;i<G[u].size();++i)
    {
        if(q[G[u][i]] == false)
        {
            dfs(G[u][i]);
        }
    }
    p[cnt++] = u;
}
void dfs2(int u)
{
    int i;
    q[u] = true;
    for(i=;i<G2[u].size();++i)
    {
        if(q[G2[u][i]] == false)
        {
            dfs2(G2[u][i]);
        }
    }
}