排序NB三人组
排序NB三人组
快速排序,堆排序,归并排序
1、快速排序

方法其实很简单:分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于6的数,再从左往右找一个大于6的数,然后交换他们。
这里可以用两个变量i和j,分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵i”和“哨兵j”。刚开始的时候让哨兵i指向序列的最左边(即i=1)
指向数字6。让哨兵j指向序列的最右边(即j=10),指向数字8。
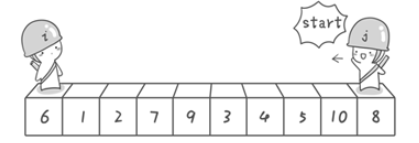
首先哨兵j开始出动。因为此处设置的基准数是最左边的数,所以需要让哨兵j先出动,这一点非常重要(请自己想一想为什么)。
哨兵j一步一步地向左挪动(即j--),直到找到一个小于6的数停下来。接下来哨兵i再一步一步向右挪动(即i++),直到找到一个数大于6的数停下来。
最后哨兵j停在了数字5面前,哨兵i停在了数字7面前。
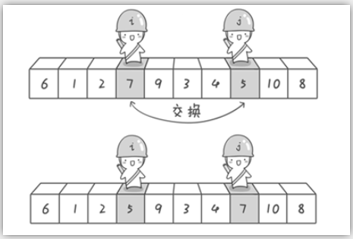
再继续:

第二次交换结束,“探测”继续。哨兵j继续向左挪动,他发现了3(比基准数6要小,满足要求)之后又停了下来。
哨兵i继续向右移动,糟啦!此时哨兵i和哨兵j相遇了,哨兵i和哨兵j都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换。交换之后的序列如下。
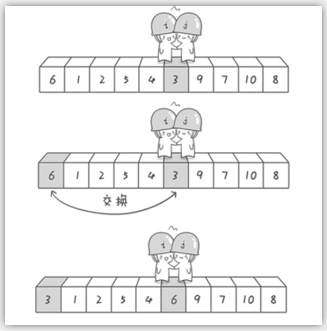
到此第一轮“探测”真正结束。此时以基准数6为分界点,6左边的数都小于等于6,6右边的数都大于等于6。回顾一下刚才的过程,
其实哨兵j的使命就是要找小于基准数的数,而哨兵i的使命就是要找大于基准数的数,直到i和j碰头为止。
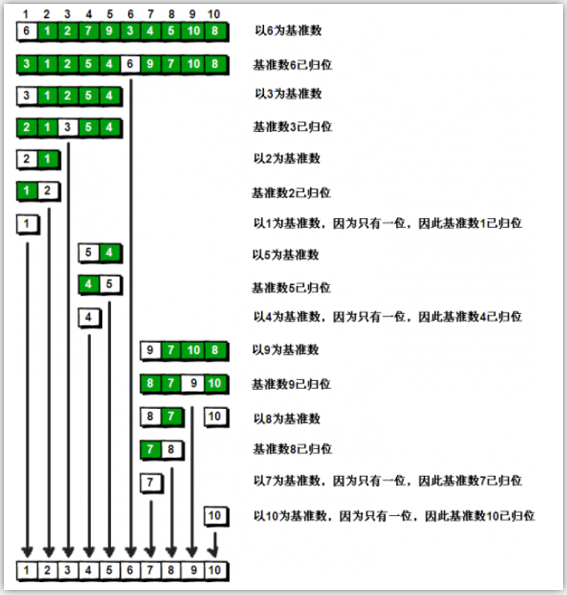
OK,解释完毕。现在基准数6已经归位,它正好处在序列的第6位。此时我们已经将原来的序列,以6为分界点拆分成了两个序列,左边的序列是“3 1 2 5 4”,右边的序列是“9 7 10 8”。接下来还需要分别处理这两个序列。因为6左边和右边的序列目前都还是很混乱的。不过不要紧,我们已经掌握了方法,接下来只要模拟刚才的方法分别处理6左边和右边的序列即可。现在先来处理6左边的序列现吧。
left right
取一个数,从左边找一个数比该数大,从右边找比该
def partition(li,left,right):
tmp = li[left]
while left<right:
while left<right and li[right]>= tmp:# 从右边找比tmp小的数
right -=1 # 往左走一步
li[left] = li[right] # 把右边的值写到左边
print(li,'right')
while left<right and li[left] <= tmp:# 从右边找比tmp大的数
left += 1
li[right] = li[left] # 把左边的值写到右边空位上
print(li,'left')
li[left] = tmp # tmp 归位
# 此时数组以 tmp为分界线,左边比tmp小,右边的比tmp大
return left
def quick_sort(li,left,right):
if left<right:
mid = partition(li,left,right)
quick_sort(li,left,mid-1)
quick_sort(li,mid+1,right)
li = [5,7,4,6,3,1,2,9,8]
quick_sort(li,0,len(li)-1)
print(li)
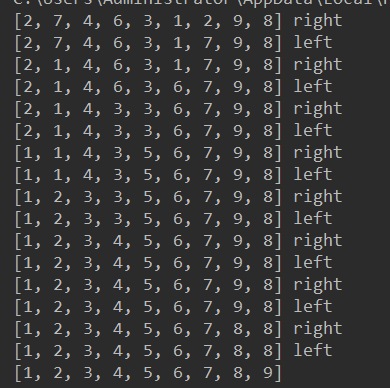

总共有logn层,每一层复杂度为n------> 时间复杂度O(nlogn)
2、堆排序
序比快速排序的时
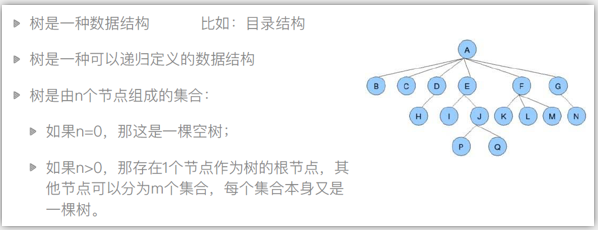

A是根节点,
叶子节点 是没有子节点的点 b c h i p q k l m n
树的深度,最深有几层,如图有4层
树的度 就是这个树最多的节点数
什么是二叉树

满二叉树和完全二叉树
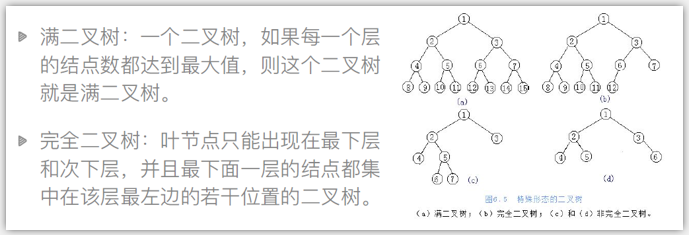
二叉树的存储方式:
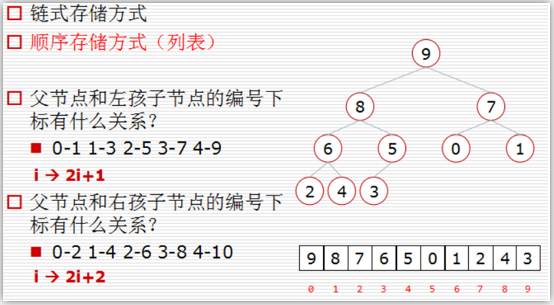
9编号为0 左孩子节点8的编号为1;右孩子7的编号为2
大根堆和小根堆

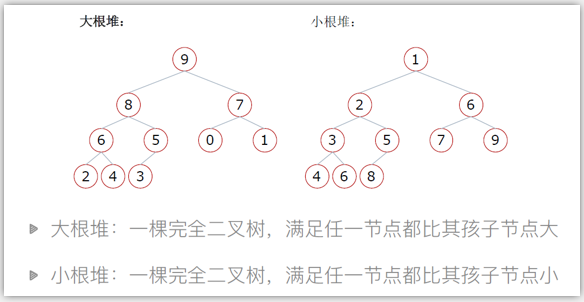
堆的概念:
堆是一个完全二叉树
堆中每一个节点的值都必须大于等于(或小于等于)其子树中每一个节点的值
---------------

其实我们的堆排序算法就是抓住了堆的这一特点,每次都取堆顶的元素,将其放在序列最后面,然后将剩余的元素重新调整为最大堆,依次类推,最终得到排序的序列。
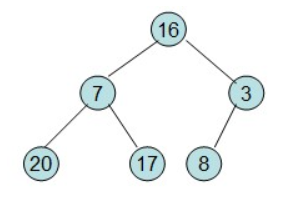
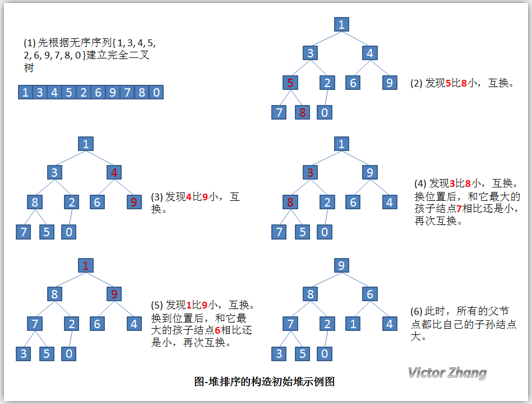
给定一个列表array=[16,7,3,20,17,8],对其进行堆排序。
首先根据该数组元素构建一个完全二叉树,得到


每次所有堆的最后一个放堆顶
i j hight都是索引值
堆建完之后堆顶是最大的元素
# 堆排序
def sift(li, low, high):
"""
:param li: 列表
:param low: 堆的根节点位置
:param high: 堆的最后一个元素的位置
:return:
"""
i = low # i最开始指向根节点 父节点
j = 2 * i + 1 # j开始是左孩子
tmp = li[low] # 把堆顶存起来
while j <= high: # 只要j位置有数
if j + 1 <= high and li[j+1] > li[j]: # 如果右孩子有并且比较大
j = j + 1 # j指向右孩子
if li[j] > tmp: # 如果左孩子或者右孩子大于tmp
li[i] = li[j] # 大的放堆顶
i = j # 往下看一层 变成新的父节点
j = 2 * i + 1 # 新的子节点
else: # tmp更大,把tmp放到i的位置上
li[i] = tmp # 把tmp放到某一级领导位置上
break
else:
li[i] = tmp # 把tmp放到叶子节点上 def heap_sort(li):
n = len(li)
# //除法不管操作数为何种数值类型,总是会舍去小数部分,返回数字序列中比真正的商小的最接近的数字。
# range(start, stop[, step])
# 比如 range(5,-1,-1) [5,4,3,2,1,0] 倒叙 # 创建堆
for i in range((n-2)//2, -1, -1):
# i表示建堆的时候调整的部分的根的下标
print(i)
sift(li, i, n-1) # 建堆完成了---挨个出数
for i in range(n-1, -1, -1):
# i 指向当前堆的最后一个元素
li[0], li[i] = li[i], li[0]
sift(li, 0, i - 1) # i-1是新的high li = [i for i in range(100)]
import random random.shuffle(li) # 打乱顺序
print(li) heap_sort(li)
print(li)
-----------

-------------------


堆排序--python内置模块
import heapq
# python 堆排序内置模块
import heapq # q-->queue优先队列
import random
li = list(range(100))
random.shuffle(li)
print(li)
heapq.heapify(li) # 建堆
n = len(li)
for i in range(n):
print(heapq.heappop(li),end=',')
堆排序-----topk问题
问题描述:有 N (N>1000000)个数,求出其中的前K个最小的数(又被称作topK问题)。

思路3:大根堆
大根堆维护一个大小为K的数组,目前该大根堆中的元素是排名前K的数,其中根是最大的数。此后,每次从原数组中取一个元素与根进行比较,如小于根的元素,则将根元素替换并进行堆调整(下沉),即保证大根堆中的元素仍然是排名前K的数,且根元素仍然最大;否则不予处理,取下一个数组元素继续该过程。该算法的时间复杂度是O(N*logK),一般来说企业中都采用该策略处理topK问题,因为该算法不需要一次将原数组中的内容全部加载到内存中,而这正是海量数据处理必然会面临的一个关卡。如果能写出代码,offer基本搞定。
# 堆排序
def sift(li, low, high):
"""
:param li: 列表
:param low: 堆的根节点位置
:param high: 堆的最后一个元素的位置
:return:
"""
i = low # i最开始指向根节点
j = 2 * i + 1 # j开始是左孩子
tmp = li[low] # 把堆顶存起来
while j <= high: # 只要j位置有数
if j + 1 <= high and li[j+1] < li[j]: # 如果右孩子有并且比较大
j = j + 1 # j指向右孩子
if li[j] < tmp: # 如果左孩子或者右孩子大于tmp
li[i] = li[j] # 大的放堆顶
i = j # 往下看一层
j = 2 * i + 1
else: # tmp更大,把tmp放到i的位置上
li[i] = tmp # 把tmp放到某一级领导位置上
break
else:
li[i] = tmp # 把tmp放到叶子节点上 def topk(li,k):
heap = li[0:k]
for i in range((k-2)//2,-1,-1):
sift(heap,i,k-1)
# 1.建堆
for i in range(k,len(li)-1):
if li[i]>heap[0]:
heap[0] = li[i]
sift(heap,0,k-1)
# 2.遍历
for i in range(k-1,-1,-1):
heap[0],heap[i] = heap[i],heap[0]
sift(heap,0,i-1) # 3.出数
return heap li = [i for i in range(100)]
import random random.shuffle(li) # 打乱顺序
# 取出前10个数
print(topk(li,10))
还有没有更简单的算法呢?答案是肯定的。
思路4:快速排序
利用快速排序的分划函数找到分划位置K,则其前面的内容即为所求。该算法是一种非常有效的处理方式,时间复杂度是O(N)(证明可以参考算法导论书籍)。对于能一次加载到内存中的数组,该策略非常优秀。如果能完整写出代码,那么相信面试官会对你刮目相看的。
归并排序
时间复杂度:O(nlogn)
空间复杂度:O(n)

假设两段有序的情况下
def merge(li,low,mid,high):
i = low
j = mid + 1
ltmp = []
while i<=mid and j<=high:
if li[i]<li[j]:
ltmp.append(li[i])
i+=1
else:
ltmp.append(li[j])
j+=1
# while 执行完,肯定有一部分没数了
while i<=mid:
ltmp.append(li[i])
i+=1
while j<=high:
ltmp.append(li[j])
j+=1
li[low:high+1]=ltmp # 归并操作,前提是列表分两段,两段分别有序
li = [2,4,5,7,1,3,6,8]
merge(li,0,3,7)
print(li)

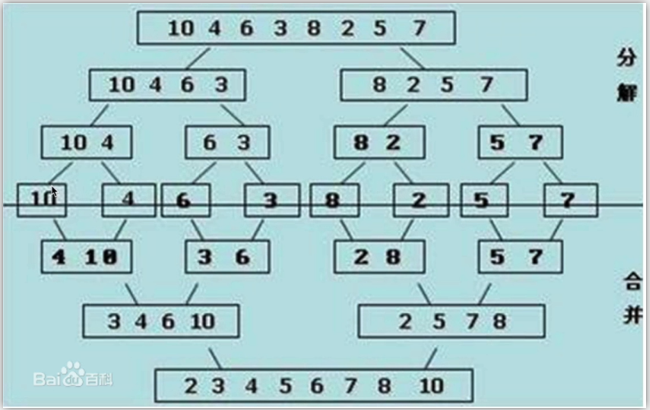
首先弄清楚递归的概念
# 递归的数据结构式栈先进后出
def calc(n):
v = int(n/2)
print(v)
if v > 0:
calc(v)
print(n) calc(10) 5
2
1
0
1
2
5
10
当遇到递归结束即然后执行递归后面的程序
print((0+1)//2) #
print((1+2)//2) #
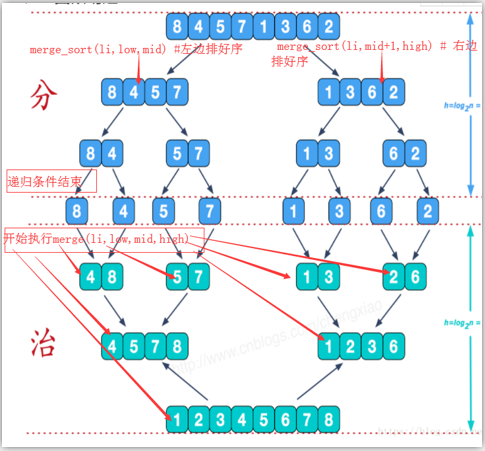
归并排序代码:
def merge(li,low,mid,high):
i = low
j = mid + 1
ltmp = []
while i<=mid and j<=high:
if li[i]<li[j]:
ltmp.append(li[i])
i+=1
else:
ltmp.append(li[j])
j+=1
# while 执行完,肯定有一部分没数了
while i<=mid:
ltmp.append(li[i])
i+=1
while j<=high:
ltmp.append(li[j])
j+=1
li[low:high+1]=ltmp
print(li) def merge_sort(li,low,high):
if low<high:#至少有两个元素
mid = (low+high)//2
# 例如len(li)==10
# mid==5
# 第一个merge_sort(li,0,5)
merge_sort(li,low,mid) # 左边排好序 # 第二个merge_sort(li,6,10)
merge_sort(li,mid+1,high) # 右边排好序
#print(li[low:high + 1])
# 当遇到low=high递归结束然后执行递归后面的程序 print(low, mid, high)
merge(li,low,mid,high) # 做归并处理 li = list(range(10))
import random
random.shuffle(li)
print(li,'初始值')
merge_sort(li,0,len(li)-1)
print(li,'最终值')
NB三人组小结

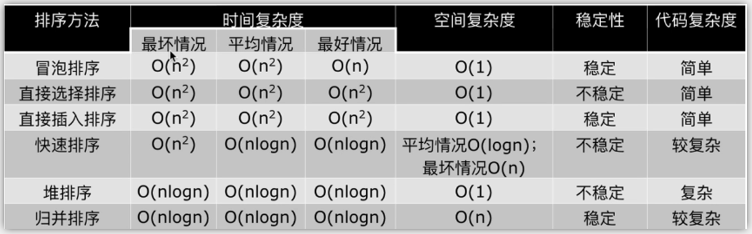
排序NB三人组的更多相关文章
- 算法排序-NB三人组
快速排序: 堆排序: 二叉树: 两种特殊二叉树: 二叉树的存储方式: 小结: 堆排序正题: 向下调整: 堆排序过程: 堆排序-内置模块: 扩展问题topk: 归并排序: 怎么使用: NB三人组小结
- 列表排序之NB三人组附加一个希尔排序
NB三人组之 快速排序 def partition(li, left, right): tmp = li[left] while left < right: while left < ri ...
- 算法 排序lowB三人组 冒泡排序 选择排序 插入排序
参考博客:基于python的七种经典排序算法 [经典排序算法][集锦] 经典排序算法及python实现 首先明确,算法的实质 是 列表排序.具体就是操作的列表,将无序列表变成有序列表! 一 ...
- 排序算法之NB三人组
快速排序 思路: 例如:一个列表[5,7,4,6,3,1,2,9,8], 1.首先取第一个元素5,以某种方式使元素5归位,此时列表被分为两个部分,左边的部分都比5小,右边的部分都比5大,这时列表变成了 ...
- 排序算法Nb三人组-归并排序
归并排序只能对两个已经有序的列表进行合并排序,所以要我们自己创建出两个有序列表.最后在进行合并. def merge2list(li1, li2): li = [] i = 0 j = 0 while ...
- 排序算法Nb三人组-快速排序
核心思想: 将列表中第一个元素拿出来,放到一边,左右两个循环,左面的大于拿出来的数,就把他挪到右面, 右面的小于拿出来的数就把他放在左面,这是列表被第一个元素''分''为两个列表,在对两个列表进行同样 ...
- 算法 排序NB二人组 堆排序 归并排序
参考博客:基于python的七种经典排序算法 常用排序算法总结(一) 序前传 - 树与二叉树 树是一种很常见的非线性的数据结构,称为树形结构,简称树.所谓数据结构就是一组数据的集合连同它们的储 ...
- 算法排序-lowB三人组
冒泡排序思路: 选择排序思路: 插入排序思路: 小结: 详细代码解释看下一篇
- 算法NB三人组
#快速排序-除了python自带的sort排序模块之外就这个最好用,只需会这个就行,其他的排序了解就好,能用冒泡,插入..的都可以用快排快速实现 import random from timewrap ...
随机推荐
- Python 解析XML实例(xml.sax)
已知movies.xml <collection shelf="New Arrivals"> <movie title="Enemy Behind&qu ...
- jQuery的遍历
jQuery有众多的方法,但是有些方法过于累赘,所以就精简了一些重要的方法,记住这些方法的(名字,功能,参数) jQuery的遍历 1.add() 将元素添加到集合中 2.children() 返回被 ...
- Ring0创建事件Ring3设置事件
同步事件(synchronizationEvent)当事件对象为激发时,如遇到KeWaitForXX等内核函数,事件对象则自动变回未激发态通知事件(NotificationEvent)当事件对象为激发 ...
- Schiff Move Free维骨力这个牌子的保健效果怎么样,是要给中老年人群服用的
Schiff Move Free维骨力这个牌子的保健效果怎么样,是要给中老年人群服用的.? https://www.zhihu.com/question/46399868 服move free还要补钙 ...
- [UE4]Format Text
蓝图会自动把字符串中的占位换成参数输入. 字符串不会自动转换,需要手动转换
- IFE2017笔记
1. jQuery.trim()方法 jQuery 杂项方法 实例 删除字符串开始和末尾的空格 2.jQuery的map方法可以批量操作数组中元素,可以替代传统在循环中处理完数据挨个push进数据的代 ...
- linux系统添加指定uid和gid的用户和组
1.添加指定gid的组 groupadd -g 1001 upload # 添加了一个指定gid为1001的upload用户 2.添加指定uid的用户,并加入到指定组 useradd -u 1001 ...
- Java基础知识_毕向东_Java基础视频教程笔记(11-12 多线程)
11天-01-多线程进程:是一个正在执行中的程序.每个进程执行都有一个执行顺序.该顺序是一个执行路径或者叫一个控制单元.线程:是进程中的一个独立的控制单元,线程在控制着进程的执行.一个进程至少有一个线 ...
- C#存储过程中传入传出参数
作者:卞功鑫 ,转载请保留http://www.cnblogs.com/BinBinGo/p/6399847.html //1 连接字符串 string connectionString = &qu ...
- 使用dtc把dtb的反编译为dts
sudo apt-get install device-tree-compiler dtc -I dtb -O dts msm8976-v1.1-qrd.dtb > msm8976-v1.1-q ...
