洛谷P2763 试题库问题(最大流)

题意

$n$道试题，每道题有多种类别属性

抽取$m$道题组成试卷，要求包含指定的类型

输出方案

Sol

又是一道zz网络流

我的构图长这样，$k_i$表示第$i$道试题需要的数量

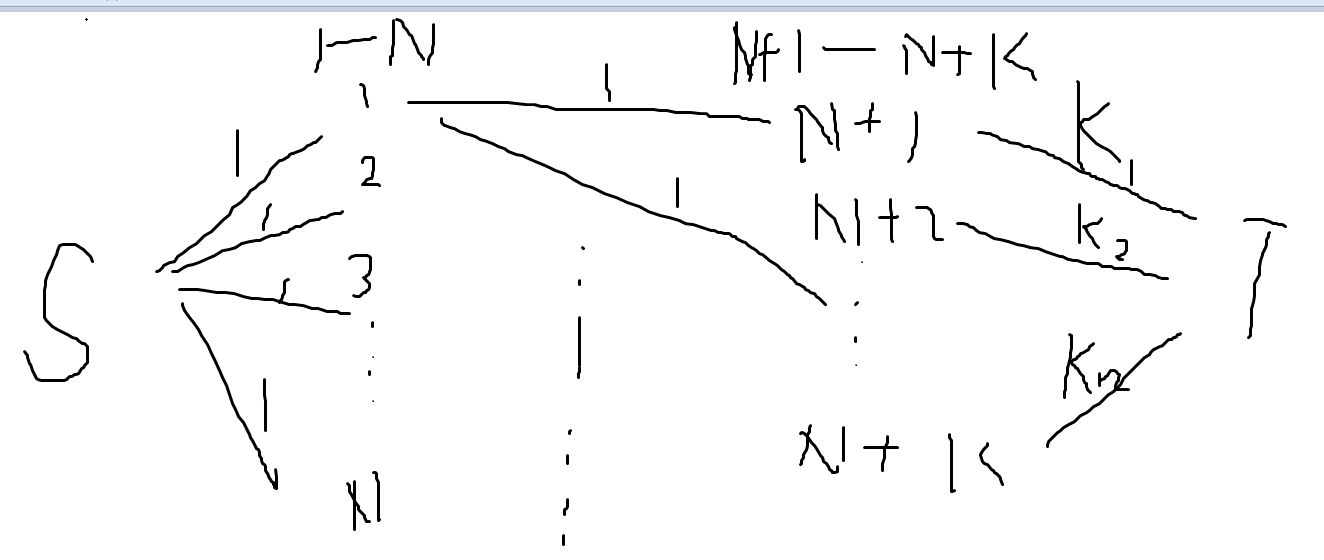
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
const int MAXN = 1e5 + , INF = 1e9 + ;
inline int read() {
    char c = getchar(); int x = , f = ;
    while(c < '' || c > '') {if(c == '-') f = -; c = getchar();}
    while(c >= '' && c <= '') x = x *  + c - '', c = getchar();
    return x * f;
}
int K, N, S, T;
int need[MAXN];
vector<int>ans[MAXN];
struct Edge {
    int u, v, f, nxt;
}E[MAXN];
int head[MAXN], cur[MAXN], num;
inline void add_edge(int x, int y, int f) {
    E[num] = (Edge){x, y, f, head[x]};
    head[x] = num++;
}
inline void AddEdge(int x, int y, int z) {
    add_edge(x, y, z);
    add_edge(y, x, );
}
int sum = , deep[MAXN];
bool BFS() {
    queue<int> q; q.push(S);
    memset(deep, , sizeof(deep)); deep[S] = ;
    while(!q.empty()) {
        int p = q.front(); q.pop();
        for(int i = head[p]; i != -; i = E[i].nxt) {
            int to = E[i].v;
            if(!deep[to] && E[i].f) {
                deep[to] = deep[p] + ;
                q.push(to);
            }
        }
    }
    return deep[T] > ;
}
int DFS(int x, int flow) {
    if(x == T) return flow;
    int ansflow = ;
    for(int &i = cur[x]; i != -; i = E[i].nxt) {
        int to = E[i].v;
        if(deep[to] == deep[x] +  && E[i].f) {
            int nowflow = DFS(to, min(flow, E[i].f));
            E[i].f -= nowflow; E[i ^ ].f += nowflow;
            ansflow += nowflow; flow -= nowflow;
            if(flow <= ) break;
        }
    }
    return ansflow;
}
int Dinic() {
    int ans = ;
    while(BFS()) {
        memcpy(cur, head, sizeof(head));
        ans += DFS(S, INF);
    }
    return ans;
}
int main() {
    memset(head, -, sizeof(head));
    K = read(); N = read(); S = ; T = N + K + ;
    int sum = ;
    for(int i = ; i <= K; i++) {
        int x = read(); sum += x;
        AddEdge(N + i, T, x);
    }
    for(int i = ; i <= N; i++) {
        int n = read();
        AddEdge(S, i, );
        for(int j = ; j <= n; j++) {
            AddEdge(i, read() + N, );
        }
    }
    if(Dinic() < sum) {puts("No Solution!"); return ;}
    for(int x = ; x <= N; x++)
        for(int i = head[x]; i != -; i = E[i].nxt)
            if(E[i].f == )
                ans[E[i].v - N].push_back(x);
    for(int i = ; i <= K; i++) {
        printf("%d: ", i);
        for(int j = ; j < ans[i].size(); j++) printf("%d ", ans[i][j]);
        puts("");
    }
    return ;
}