Codeforces Round #344 (Div. 2) E. Product Sum 二分斜率优化DP

E. Product Sum

 

Blake is the boss of Kris, however, this doesn't spoil their friendship. They often gather at the bar to talk about intriguing problems about maximising some values. This time the problem is really special.

You are given an array a of length n. The characteristic of this array is the value 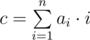 — the sum of the products of the valuesai by i. One may perform the following operation exactly once: pick some element of the array and move to any position. In particular, it's allowed to move the element to the beginning or to the end of the array. Also, it's allowed to put it back to the initial position. The goal is to get the array with the maximum possible value of characteristic.

Input

The first line of the input contains a single integer n (2 ≤ n ≤ 200 000) — the size of the array a.

The second line contains n integers ai (1 ≤ i ≤ n, |ai| ≤ 1 000 000) — the elements of the array a.

Output

Print a single integer — the maximum possible value of characteristic of a that can be obtained by performing no more than one move.

Examples

input

4
4 3 2 5

output

39

Note

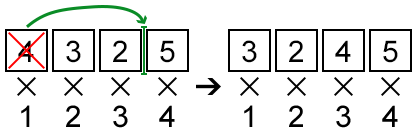
In the first sample, one may pick the first element and place it before the third (before 5). Thus, the answer will be3·1 + 2·2 + 4·3 + 5·4 = 39.

In the second sample, one may pick the fifth element of the array and place it before the third. The answer will be1·1 + 1·2 + 1·3 + 2·4 + 7·5 = 49.

题意：

　　给你一个序列a，让你求∑ a[i]*i 是多少

　　你可以进行一次操作：将任意位置的一个数组元素拿出来再插入任意一个新的位置或者不进行此操作。

　　问你最大的∑ a[i]*i 是多少。

题解：

　　首先假设拿出元素向前面的位置插入

　　那么 dp[i] = max(pre[i-1]+i*a[i],pre[i-1]+sum[i-1]-sum[j-1] +j*a[i]);

　　pre表示前缀答案和，sum表示数组前缀和，这个转移方程是可以用斜率优化的，只不过斜率并不满足单调性质，那么我们就要手动维护一个凸包来二分找答案了。。。

　　拿元素向后插是一样的道理

#include<bits/stdc++.h>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define ls i<<1
#define rs ls | 1
#define mid ((ll+rr)>>1)
#define pii pair<int,int>
#define MP make_pair
typedef long long LL;
const long long INF = 1e18+1LL;
const double Pi = acos(-1.0);
const int N = 2e5+, M = 1e3+, mod = 1e9+, inf = 2e9+;

LL dp1[N],dp2[N],sum[N],las[N],pre[N];
LL splopex(int i,int j) {
    return sum[i-] - sum[j-];
}
LL splopey(int i,int j) {
    return i - j;
}
int n,a[N],q[N];
int main() {
        scanf("%d",&n);
        for(int i = ; i <= n; ++i) scanf("%d",&a[i]);
        for(int i = ; i <= n; ++i) sum[i] = sum[i-] + a[i];
        int head =  , tail = ;
        las[] = ;
        for(int i = ; i <= n; ++i) {
            dp1[i] = las[i-] + 1LL * i * a[i];
            las[i] = dp1[i];
            if(head == tail) {q[tail++] = i;continue;}
            int l = head, r = tail-,md;
            while( l < r ) {
                md =  (l+r)>>;
                if(md +  < tail && splopex(q[md+],q[md]) < 1LL*splopey(q[md+],q[md])*a[i])
                    l = md + ;
                else
                    r = md;
            }
            md = r;
            dp1[i] = max(las[i-] + 1LL * sum[i-] - 1LL * sum[q[md]-] + 1LL*q[md]*(a[i]),dp1[i]);
            while(head + <tail && splopey(i,q[tail-])*splopex(q[tail-],q[tail-])
                                >= splopey(q[tail-],q[tail-])*splopex(i,q[tail-])) tail--;
            q[tail++] = i;
        }

        pre[n+] = ;
        head = , tail = ;
        for(int i = n; i >= ; --i) {
            dp2[i] = pre[i+] + 1LL * i * a[i];
            pre[i] = dp2[i];
            if(head == tail) {q[tail++] = i;continue;}
            int l = head, r = tail-,md;
            while( l < r ) {
                md =  (l+r)>>;
                if(md +  < tail && splopex(q[md+]+,q[md]+) < 1LL*splopey(q[md+],q[md])*a[i])
                    l = md + ;
                else
                    r = md;
            }
            md = r;
            dp2[i] = max(pre[i+] - 1LL * sum[q[md]] + 1LL * sum[i] + 1LL*q[md]*(a[i]),dp2[i]);
            while(head + <tail && splopey(i,q[tail-])*splopex(q[tail-]+,q[tail-]+)
                                <= splopey(q[tail-],q[tail-])*splopex(i+,q[tail-]+)) tail--;
            q[tail++] = i;
        }
        LL ans = -INF;
        for(int i = ; i <= n; ++i) {
            ans = max(ans, max(dp1[i]+pre[i+],dp2[i]+las[i-]));
        }
        cout<<ans<<endl;
    return ;
}